논문 리뷰: A deep reinforcement learning assisted simulated annealing algorithm for a maintenance planning problem (2022 Feb)

https://link.springer.com/article/10.1007/s10479-022-04612-8

Abstract

Maintenance planning aims to improve the reliability of assets, prevent the occurrence of asset failures, and reduce maintenance costs associated with downtime of assets and maintenance resources (such as spare parts and workforce). Thus, effective maintenance planning is instrumental in ensuring high asset availability with the minimum cost. Nevertheless, to find such optimal planning is a nontrivial task due to the (i) complex and usually nonlinear inter-relationship between different planning decisions (e.g., inventory level and workforce capacity), and (ii) stochastic nature of the system (e.g., random failures of parts installed in assets). To alleviate these challenges, we study a joint maintenance planning problem by considering several decisions simultaneously, including workforce planning, workforce training, and spare parts inventory management.

• 유지보수 계획(Maintenance planning)은 자산의 신뢰성을 향상, 자산 고장을 방지, 자산 및 유지보수 자원의 다운타임과 관련된 유지 보수 비용을 줄이는 것을 목표로 함
• 효과적인 유지보수 계획은 최소 비용(minimum cost)으로 높은 자산 가용성(high asset availability)을 보장하는 것이 중요함
• 이러한 계획을 찾는 것은 아래 이유로 인해 어려움
  • 다양한 계획 결정(재고 수준 및 인력 용량)간의 복잡하고 일반적으로 비선형적인 상호 관계
  • 시스템의 확률적 특성(부품의 무작위 고장)
• 문제를 완화하기 위해 인력 계획, 인력 교육 및 예비 부품 재고 관리를 포함한 여러 결정을 동시에 고려하여 공동 유지보수 계획 문제를 연구

 

We develop a hybrid solution algorithm (DRLSA) that is a combination of Double Deep Q-Network based Deep Reinforcement Learning (DRL) and Simulated Annealing (SA) algorithms.

• Double Deep Q-Network 기반 DRL과 SA를 결합한 하이브리드 솔루션 알고리즘인 DRLSA를 개발

 

In each episode of the proposed algorithm, the best solution found by DRL is delivered to SA to be used as an initial solution, and the best solution of SA is delivered to DRL to be used as the initial state. Different from the traditional SA algorithms where neighborhood structures are selected only randomly, the DRL part of DRLSA learns to choose the best neighborhood structure to use based on experience gained from previous episodes.

• 제안된 알고리즘의 각 에피소드에서 DRL에서 찾은 최상의 솔루션(best solution)이 SA에 전달되어 초기 솔루션(initial solution)으로 사용
• SA의 최상의 솔루션이 DRL에 전달되어 초기 상태(initial state)로 사용
• 기존의 SA 알고리즘에서는 이웃 구조(neighborhood structures)가 무작위로 선택됨
• DRLSA의 DRL 부분은 이전 에피소트에서 얻은 경험을 기반으로 사용할 최상의 이웃 구조를 선택하는 방법을 학습함

 

We compare the performance of the proposed solution algorithm with several well-known meta-heuristic algorithms, including Simulated Annealing, Genetic Algorithm (GA), and Variable Neighborhood Search (VNS). Further, we also develop a Machine Learning (ML) algorithm (i.e., K-Median) as another benchmark in which different properties of spare parts (e.g., failure rates, holding costs, and repair rates) are used as clustering features for the ML algorithm.

• 제안된 솔루션 알고리즘(DRLSA)의 성능을 Simulated Annealing(SA), Genetic Algorithm(GA), Variable Neighborhood Search (VNS)를 포함한 여러 메타 휴리스틱(meta-heuristic) 알고리즘과 비교
• 새로운 벤치마크인 ML 알고리즘 (K-Median)을 개발함
  • 예비 부품의 다양한 속성(고장률, 유지 비용, 복구율 등)이 ML 알고리즘을 위한 클러스터링 기능으로 사용됨

 

Our study reveals that the DRLSA finds the optimal solutions for relatively small-size instances, and it has the potential to outperform traditional meta-heuristic and ML algorithms.

• DRLSA가 비교적 작은 크기의 인스턴스에 대해 최적의 솔류션을 찾고 기존의 메타 휴리스틱 및 ML 알고리즘을 능가할 가능성이 있음

 

1. Introduction

Downtime is described as the accumulated amount of time when an asset is out of action or unavailable for use. It is required to keep the asset downtime under 10% to achieve world-class standards (Ong et al. 2020). Unplanned downtime due to asset failures can be very expensive. It is estimated that the average cost of unplanned downtime is $260,000 per hour across all industries (Arsenault 2016). Further, the downtime cost in terms of revenue lost per hour may vary depending on the industry. For example, while it is $2.1 million for pharmaceuticals, it reaches up to $4.6 million for the telecommunications industry (Hicks 2019).

• 다운타임: 자산이 작동하지 않거나 사용할 수 없을 때의 누적 시간.
• 세계 최고 수준의 표준을 달성하기 위해서는 자산 다운타임을 10% 미만으로 유지하는 것이 요구됨
• 계획되지 않은 다운타임은 매우 비용이 소모
• 계획되지 않은 다운타임의 평균 비용은 전 산업에서 시간당 26만 달러로 추정되지만, 다운타임 비용은 산업에 따라 다를 수 있음. (예를 들어, 의약품의 경우 $2.1M, 통신산업 $4.6만)

 

Developing proper maintenance strategies is essential to reduce both the unplanned downtime and the operational costs of the assets. Maintenance strategies are broadly classified into two categories, namely, corrective maintenance and preventive maintenance (Rahmati et al. 2018). The corrective maintenance, which is also called breakdown maintenance, is performed after the failure and tries to bring the failed asset up to its operational status. Corrective maintenance is a reactive strategy. Thus, it can lead to high asset downtime and maintenance costs, if implemented improperly (Salari and Makis 2020). In this paper, we try to find a cost-effective implementation of the corrective maintenance by simultaneously optimizing different (but interconnected) planning decisions.

• 계획되지 않은 다운타임과 자산의 운영 비용을 모두 줄이기 위해서는 적절한 유지 보수 전략을 개발
• 유지 보수 전략은 크게 두 가지로 분류
  • 시정 유지보수(고장 유지보수)
    • 장애 발생 후 수행되며 장애가 발생한 자산을 운영 상태로 복구하는 것
    • 시정 유지 보수는 반응형 전략임
    • 부적절하게 구현될 경우 높은 자산 다운타임과 유지 보수 비용을 초래할 수 있음
  • 예방 유지보수
• 본 논문에서는 서로 다른(그러나 상호 연결된) 계획 결정을 동시에 최적화하여 시정 유지 보수의 비용 효율적인 구현을 찾으려고 함

 

Among the aforementioned planning decisions, spare part inventory decisions have paramount importance since the unavailability of spare parts is the major reason for all asset downtime (Turan et al. 2020a; Kosanoglu et al. 2018). Holding a sufficient number of spare part stocks in inventory may reduce the asset downtime. However, many spare parts are expensive and it is economically more feasible to repair the failed parts/components of assets rather than replacing them with spares (Samouei et al. 2015; Levner et al. 2011). A failed part that can be repaired to an as-good-as-new condition is called a “repairable" part. In this paper, we optimize the number of repairable spare part stocks to keep in the inventory.

• 예비 부품(spare parts)의 가용성이 모든 자산 다운타임의 주요 원인 → 예비 부품 재고 결정이 가장 중요
• 재고에 충분한 수의 예비 부품 재고를 보유하게 되면 자산 다운타임이 감소하지만 많은 예비 부품이 고가이며 고장 부품을 예비 부품으로 교체보다 수리가 저렴함
• 고장 부품을 양호한 상태로 수리할 수 있는 것을 수리 가능한(repairable) 부품이라고 합니다.
• Task 1. 재고를 유지하기 위해 수리 가능한 예비 부품 재고 수를 최적화

 

When a repairable part installed inside an asset fails, the defective part is substituted with a new one from the spare parts inventory (if there is any available) and the failed part is shipped to the maintenance/repair facility. In the maintenance facility, the failed part is repaired by the skilled maintenance workforce, afterwards, it is placed in spare stock inventory to be eventually used in case of another asset failure (Samouei et al. 2015; Turan et al. 2020b). It is clear that the maintenance workforce capacity (i.e., the number of technicians and their skills) in the repair facility directly affects the number of spare parts to keep in the inventory. In other words, a high number of skilled workforce would lead to faster repairs for failed parts and reduce throughput times in the maintenance facility, which would result in achieving the same availability level for assets with a less number of spare stocks. Thus, we include the maintenance workforce capacity optimization in our problem as the second planning decision.

• 자산 내부 수리 가능 부품에 고장이 발생 → 고장 부품은 예비 부품 창고에서 예비 부품으로 교체되고(사용 가능한 경우), 고장 부품은 수리 시설로 출하
• 정비 시설에서 고장 부품은 숙련된 정비 인력에 의해 수리되고, 이후 다른 자산 고장이 발생 시 사용될 예비 재고 창고에 배치
• 유지보수 시설의 정비 인력 용량(기술자 수)은 재고에 보관해야 할 예비 부품 수에 직접적인 영향을 미침. 숙련된 인력이 많으면 고장 부품의 수리 속도가 빨라지고 유지보수 시설의 처리량 시간이 단축되어 예비 재고가 적은 자산에도 동일한 가용성 수준을 달성할 수 있음
• Task 2. 정비 인력 용량(maintenance workforce capacity) 최적화

 

It is generally assumed that all workforce in the maintenance facility has the same skill set and can repair all types of failed parts (i.e., full cross-training) in the system (Sleptchenko et al. 2019). Nevertheless, limited workforce flexibility with appropriate cross-training can offer most of the benefits of full cross-training (Jordan and Graves 1995). Moreover, if the repair tasks are complex and varied, utilizing full cross-trained maintenance workers may not be economical due to the limited learning capacity of workers and associated high training costs (Wang and Tang 2020). As our third maintenance planning decision, we aim at optimizing the skill assignment of the maintenance workforce. That is, we try to determine the skill set in which each worker can only repair a subset of all part types to minimize downtime with the minimum cost.

• 일반적으로 유지보수 시설의 모든 인력은 동일한 기술 집합을 가지고 있으며 시스템에서 모든 유형의 고장 부품을 수리할 수 있다고 가정(전체 교차 교육 full cross-training)
• 그럼에도 불구하고 적절한 교차 교육을 통한 제한된 인력 유연성은 전체 교차 교육의 대부분의 이점을 제공할 수 있음. 또한 수리 작업이 복잡하고 다양한 경우 전체 교차 교육을 받은 유지 보수 인력을 활용하는 것은 근로자의 학습 용량이 제한되고 관련된 높은 교육 비용으로 인해 비경제적임(비쌈)
• Task 3. 유지 보수 인력(maintenance workforce)의 기술 할당을 최적화 (각 근로자가 모든 부품 유형의 하위 집합만 수리할 수 있는 기술 집합을 결정)

 

We contribute to the literature by addressing all the above-listed planning decisions in a single joint optimization model. Solving the modeled joint problem and finding the (near) optimal maintenance plans are nontrivial tasks due to the challenges associated with (i) the size of the decision space to search for (i.e., the number of feasible plans including, amount of spare stocks to keep on inventory for each part type, the number of maintenance workers to utilize in the maintenance facility and the number of possible combinations of assignments of skills to workers), and (ii) the stochastic nature of the system (e.g., random failures of parts installed in assets and service rate of maintenance).

• single joint 최적화 모델에서 위에 나열된 모든 계획 결정을 해결하고자 함
• 모델링된 공동 문제를 해결하고 (근접한) 최적의 유지 관리 계획을 찾는 것 어려움
  • 1) 검색할 의사결정 공간의 크기(부품 유형별 재고를 유지할 예비 재고량, 유지보수 시설 내 유지보수 작업자 수, 작업자 기술 할당 조합 수를 포함한 실현 가능(possible)한 계획 수)
  • 2) 시스템의 확률적 특성(자산 내 부품의 무작위 고장 및 유지보수의 service rate)

 

To handle the challenge (i), we enhance a well-known meta-heuristic algorithm to search solution space more effectively. In this direction, we couple a Double Deep Q-Network based Deep Reinforcement Learning (DRL) and a Simulated Annealing (SA) algorithm. In this coupling, different from the traditional SA algorithms where neighborhood structures are selected only randomly, DRL learns to choose the best neighborhood structure based on experience gained from previous episodes and delivers the selected neighborhood structure to SA to use in future iterations.

To overcome the challenge (ii), we model the maintenance facility as a queuing network. However, when the model’s size gets larger (i.e., the number of spare part types and the number of workers), finding closed-form solutions for the modeled queuing network gets computationally demanding. Thus, we alleviate this difficulty by dividing the maintenance facility into smaller and independent repair cells where each repair cell is responsible for repairing a subset of all part types with its own cross-trained workforce.

 

 

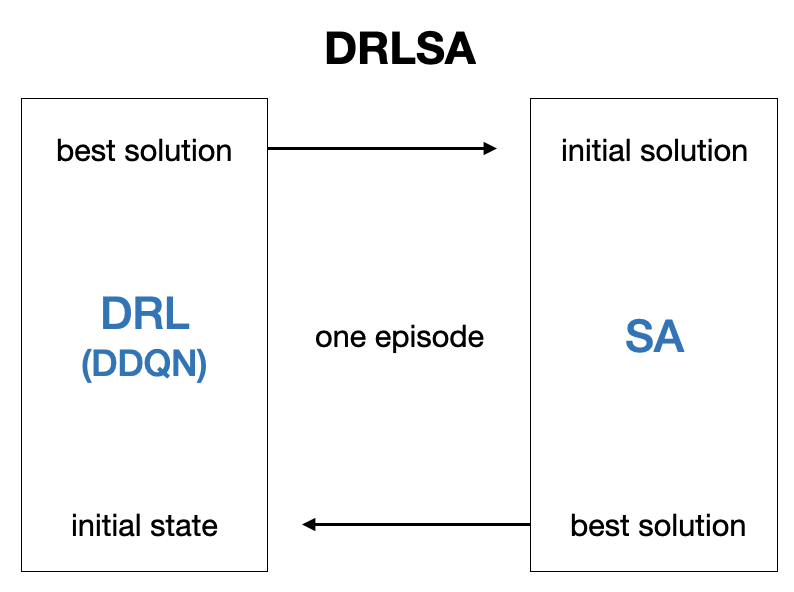
• Task (i)를 해결하기 위해 잘 알려진 메타 휴리스틱 알고리즘을 개선하여 해 공간을 보다 효과적으로 검색 → DDQN 기반 DRL과 SA 알고리즘을 결합. 랜덤으로 이웃 구조를 선택하는 기존 SA 알고리즘과 달리 DRL은 이전 에피소드에서 얻은 경험을 기반으로 가장 적합한 이웃 구조를 선택하는 방법을 학습, 선택한 이웃 구조를 SA에 전달하여 향후 반복에 사용함
• Task (ii)를 극복하기 위해 유지 보수 시설을 큐잉 네트워크로 모델링. 그러나 모델의 크기가 커지면(예: 예비 부품 유형 및 작업자 수) 큐잉 네트워크에 대한 closed-form 해를 찾는 것은 계산적으로 어려움. 따라서 유지 보수 시설을 더 작은 독립적인 복구 셀로 분할하여 각 복구 셀이 자체의 교차 교육된 인력으로 모든 부품 유형의 하위 집합을 복구하는 역할을 수행함으로써 이러한 어려움을 해결

 

The remainder of this paper is organized as follows. In Sect. 2, we review the relevant literature on deep reinforcement learning in maintenance problems. We also briefly discuss how deep reinforcement learning has been integrated with different optimization algorithms to solve hard optimization problems. In Sect. 3, the details of the problem are provided and the mathematical model is introduced. Next, we present the details of the solution algorithm in Sect. 4. We list and briefly discuss the benchmark algorithms and methods in Sect. 5. In Sect. 6, we outline the computational experiment design and present both computational and managerial results. Lastly, we discuss conclusions and future research directions in Sect. 7.

• 이 논문의 나머지 부분은 다음과 같이 구성됨. 2절에서는 유지 보수 문제의 심층 강화 학습에 대한 관련 문헌을 검토합니다. 또한 심층 강화 학습이 다양한 최적화 알고리즘과 통합되어 하드 최적화 문제를 해결하는 방법에 대해서도 간략하게 논의합니다. 3절에서는 문제의 세부 사항이 제공되고 수학적 모델이 소개됩니다. 다음으로 4절의 솔루션 알고리즘 세부 사항을 제시합니다. 5절의 벤치마크 알고리즘 및 방법을 나열하고 간략하게 논의합니다. 6절에서는 계산 실험 설계의 개요를 설명하고 계산 및 관리 결과를 모두 제시합니다. 마지막으로 7절의 결론과 향후 연구 방향에 대해 논의합니다.

 

2. Literature Review

Reinforcement Learning (RL) and Deep Reinforcement Learning (DRL) have gained pop- ularity in solving hard combinatorial optimization problems. In this section, we review the RL-DRL in combinatorial optimization and present a summarized literature review of the works in maintenance that employ RL-DRL as a solution approach in Table 1.

• 강화 학습(RL)과 심층 강화 학습(DRL)은 어려운 조합 최적화 문제를 해결하는 데 있어 인기를 얻었습니다. 이 섹션에서는 조합 최적화에서 RL-DRL을 검토하고 표 1에서 RL-DRL을 솔루션 접근 방식으로 사용하는 유지 보수 작업에 대한 요약 문헌 검토를 제시합니다.

 

RL has shown promising results to solve complex combinatorial optimization problems. Integration of RL into optimization has been through two different patterns (Mazyavkina et al. 2020). In the first stream, the decision-maker can exploit the RL methods to directly find the part of the solution or the complete solution without any off-the-shelf solver (end to end learning) (Bengio et al. 2020). In this setting, RL has been employed to tackle many combinatorial optimization problems, such as Travelling Salesman Problem (TSP) (Bello et al. 2017; Kool et al. 2019; Emami and Ranka 2018; Ma et al. 2019; Deudon et al. 2018), Vehicle Routing Problem (VRP) (Nazari et al. 2018; Kool et al. 2019), and Bin Packing Problems (BPP) (Hu et al. 2017; Duan et al. 2019). Further examples of RL applications to optimization include traffic flow optimization (Walraven et al. 2016), pricing strategy optimization (Krasheninnikova and García 2019), bioprocess optimization (Petsagkourakis et al. 2020), and orienteering problem (Gama and Fernandes 2020).

• RL은 복잡한 조합 최적화 문제를 해결하는 데 유망한 결과를 보여주었습니다. 최적화에 RL을 통합하는 것은 두 가지 다른 패턴을 통해 이루어졌습니다(Mazyavkina et al. 2020). 첫 번째 스트림에서 의사 결정자는 RL 방법을 활용하여 기성 해결사(end to end learning) 없이 솔루션 또는 완전한 솔루션의 부분을 직접 찾을 수 있습니다(Bengio et al. 2020). 이 환경에서 RL은 Travelling Salemen Problem(TSP)(Bello et al. 2017; Kool et al. 2019; Emami and Ranka 2018; Ma et al. 2019; Deudon et al. 2018), 차량 라우팅 문제(VRP)(Nazari et al. 2018; Kool et al. 2019) 및 빈 패킹 문제(BPP)(Hu et al. 2017; Duan et al. 2019). 최적화에 대한 RL 적용의 추가 예로는 트래픽 흐름 최적화(Walraven et al. 2016), 가격 전략 최적화(Krasheninnikova and García 2019), 바이오 프로세스 최적화(Petsagkourakis et al. 2020) 및 오리엔티어링 문제(Gama and Fernandes 2020)가 있습니다.

 

Table 1  A summarized review of the literature on reinforcement-deep reinforcement learning in maintenance

Another form is utilizing RL methods to improve the solution abilities of already existing solvers. In this approach, the optimization algorithm can call RL one time to initialize some parameter values or can call it repeatedly as the optimization algorithm iterates (Bengio et al. 2020). In this framework, RL methods are used to leverage the power of solvers or problem- specific solution heuristics by initializing values of some hyper-parameters. For example, RL can be utilized to select the branching variable in MIP solvers (Etheve et al. 2020; Hottung et al. 2020; Tang et al. 2020). Some recent studies of Ma et al. (2019); Deudon et al. (2018); Chen and Tian (2019) show that optimization heuristics powered with RL methods outperform previous methods.

• 또 다른 형태는 RL 방법을 사용하여 이미 존재하는 해결사의 솔루션 능력을 향상시키는 것입니다. 이 접근법에서 최적화 알고리즘은 RL을 한 번 호출하여 일부 매개변수 값을 초기화하거나 최적화 알고리즘이 반복적으로 호출할 수 있습니다(Bengio et al. 2020). 이 프레임워크에서 RL 방법은 일부 하이퍼 파라미터의 값을 초기화하여 해결사 또는 문제별 솔루션 휴리스틱스의 힘을 활용하는 데 사용됩니다. 예를 들어, RL은 MIP 해결사에서 분기 변수를 선택하는 데 활용될 수 있습니다(Ethve et al. 2020; Hottung et al. 2020; Tang et al. 2020). Ma et al. (2019); Deudon et al. (2018); Chen and Tian (2019)에 대한 일부 최근 연구에 따르면 RL 방법으로 구동되는 최적화 휴리스틱스가 이전 방법보다 성능이 우수한 것으로 나타났습니다.

 

Deep reinforcement learning (DRL) is one of the most intriguing areas of machine learning that combines reinforcement learning and deep learning. In particular, Deep Neural Network (DNN) allows reinforcement learning to be applied to complicated problems due to its ability to learn different levels of perception from data (François-Lavet et al. 2018). The benefits brought by DRL to other fields such as robotics and computer games are also employed to solve complex decision-making problems. Some recent works use DRL to solve some of the most prominent complex optimization problems such as resource management problems (Mao et al. 2016), job scheduling (Chen et al. 2017; Liu et al. 2020; Liang et al. 2020), VRP (Nazari et al. 2018; Lin et al. 2020; Zhao et al. 2020; Yu et al. 2019), and production scheduling problems (Waschneck et al. 2018b, a; Hubbs et al. 2020).

• 심층 강화 학습(DRL)은 강화 학습과 심층 학습을 결합한 기계 학습의 가장 흥미로운 분야 중 하나입니다. 특히, 심층 신경망(DNN)은 데이터로부터 다양한 인식 수준을 학습할 수 있기 때문에 강화 학습을 복잡한 문제에 적용할 수 있습니다(François-Lavet et al. 2018). DRL이 로봇 공학 및 컴퓨터 게임과 같은 다른 분야에 제공하는 이점은 복잡한 의사 결정 문제를 해결하는 데도 사용됩니다. 일부 최근 작업은 DRL을 사용하여 자원 관리 문제(Mao et al. 2016), 작업 스케줄링 문제(Chen et al. 2017; Liu et al. 2020; Liang et al. 2020), VRP(Nazari et al. 2018; Lin et al. 2020; Zhao et al. 2020; Yu et al. 2019) 및 생산 스케줄링 문제(Washneck et al. 2018b, a; Hubbs et al. 2020)와 같은 가장 중요한 복잡한 최적화 문제를 해결합니다.

 

The maintenance planning (e.g., frequencies of corrective and preventive maintenance and condition-based maintenance policies) of spare parts inventory management models is well-studied in the literature with the various optimization models. Most of those studies employ off-the-shelf optimization software, heuristics, and well-known meta-heuristics (i.e., SA, Genetic Algorithm, Variable Neighborhood Search, etc.). Besides these methods, DRL is a promising new method in maintenance planning. Some recent studies employ RL to solve maintenance planning problems in various sectors. Huang et al. (2020) propose a preventive maintenance (PM) model in the Markov Decision Process (MDP) framework and solve the resulting problem employing the DRL algorithm. Andriotis and Papakonstantinou (2019) study a PM and inspection model for large multi-component engineering systems. They model a sequential decision-making problem with the MDP concept and propose a DRL algorithm that is capable of solving problems with massive state space.

• 예비 부품 재고 관리 모델의 유지 보수 계획(예: 시정 및 예방 유지 보수 빈도 및 상태 기반 유지 보수 정책)은 다양한 최적화 모델과 함께 문헌에 잘 연구되어 있습니다. 이러한 연구의 대부분은 기성 최적화 소프트웨어, 휴리스틱 및 잘 알려진 메타 휴리스틱(즉, SA, 유전 알고리즘, 가변 이웃 검색 등)을 사용합니다. 이러한 방법 외에도 DRL은 유지 보수 계획에서 유망한 새로운 방법입니다. 일부 최근 연구에서는 RL을 사용하여 다양한 부문의 유지 보수 계획 문제를 해결합니다. Huang et al. (2020)은 MDP(Markov Decision Process) 프레임워크에서 예방적 유지 보수(PM) 모델을 제안하고 DRL 알고리즘을 사용하여 결과적인 문제를 해결합니다. Andriotis와 Papakonstantinou (2019)는 대형 멀티 컴포넌트 엔지니어링 시스템의 PM 및 검사 모델을 연구합니다. 이들은 MDP 개념으로 순차적 의사 결정 문제를 모델링하고 방대한 상태 공간의 문제를 해결할 수 있는 DRL 알고리즘을 제안합니다.

 

Zhang et al. (2019) study the prediction of the equipment’s remaining useful life, which is an essential indicator in maintenance planning. They model this problem as Health Indicator Learning (HIL) which learns a health curve that shows the equipment health conditions over time. Instead of conventional methods (inspection by hand or physical modeling) in addressing HIL, they propose a data-driven model that employs the DRL method. Hoong Ong et al. (2020) utilize sensor data to evaluate the equipment health condition and obtain optimal maintenance policy by DRL approach. Similarly, Skordilis and Moghaddass (2020) employ sensor data for a real-time decision-making framework for system maintenance based on DRL. Some other recent works use DRL to solve PM planning problems for different domains such as energy (Rocchetta et al. 2019), infrastructure (Wei et al. 2020; Yao et al. 2020), aero-engine (Li et al. 2019), and cybersecurity (Allen et al. 2018).

• Zhang et al. (2019)는 유지 보수 계획의 필수 지표인 장비의 남은 유효 수명 예측을 연구합니다. 그들은 이 문제를 시간에 따라 장비 상태를 보여주는 상태 곡선을 학습하는 HIL(Health Indicator Learning)로 모델링합니다. 그들은 HIL을 해결하는 기존 방법(손으로 검사하거나 물리적 모델링) 대신 DRL 방법을 사용하는 데이터 기반 모델을 제안합니다. Hoong Ong et al. (2020)은 센서 데이터를 활용하여 장비 상태를 평가하고 DRL 접근 방식으로 최적의 유지 보수 정책을 얻습니다. 마찬가지로 Skordilis와 Moghadass (2020)는 DRL을 기반으로 시스템 유지 보수를 위한 실시간 의사 결정 프레임워크에 센서 데이터를 사용합니다. 최근 일부 다른 작업은 DRL을 사용하여 에너지(Rocchetta et al. 2019), 인프라(Wei et al. 2020; Yao et al. 2020), 에어로 엔진(Li et al. 2019) 및 사이버 보안(Allen et al. 2018)과 같은 다양한 도메인의 PM 계획 문제를 해결합니다.

 

As IoT-based monitoring routine increases, intensive data-driven condition-based main- tenance (CBM) planning gains increasing attention in recent years. Some recent studies show that using the benefits of RL techniques (such as learning from historical and online data) in CBM planning may accommodate promising results. Zhang and Si (2020) propose a CBM planning model for multi-component systems which can utilize equipment conditions at each inspection directly in decision-making without maintenance thresholds. Instead of computationally inefficient and intractable conventional threshold methods, they employ a DRL-based method. Mahmoodzadeh et al. (2020) study an RL-based CBM planning model for corrosion-related maintenance management of dry gas pipelines.

• IoT 기반 모니터링 루틴이 증가함에 따라 최근 몇 년 동안 집중적인 데이터 기반 상태 유지 관리(CBM) 계획에 대한 관심이 높아지고 있습니다. 일부 최근 연구에 따르면 CBM 계획에서 RL 기술(예: 과거 및 온라인 데이터에서 학습)의 이점을 사용하면 유망한 결과를 수용할 수 있습니다. Zhang과 Si(2020)는 유지 관리 임계값 없이 각 검사에서 장비 조건을 의사 결정에 직접 활용할 수 있는 다성분 시스템에 대한 CBM 계획 모델을 제안합니다. 계산적으로 비효율적이고 다루기 힘든 기존 임계값 방법 대신 DRL 기반 방법을 사용합니다. Mahmoodzadeh et al.(2020)은 건식 가스 파이프라인의 부식 관련 유지 관리를 위한 RL 기반 CBM 계획 모델을 연구합니다.

 

The literature review in RL-DRL in maintenance optimization reveals the vacancy of research on the DRL-based solution approaches to corrective maintenance planning. This study contributes to maintenance planning optimization by developing a hybrid solution algorithm that combines Deep Reinforcement Learning (DRL) and Simulated Annealing (SA) algorithm.

• 유지보수 최적화에서 RL-DRL의 문헌고찰은 DRL 기반 솔루션 접근법을 수정 유지보수 계획에 대한 연구의 공백을 보여줍니다. 본 연구는 DRL(Deep Reinforcement Learning)과 SA(Mulated Annealing) 알고리즘을 결합한 하이브리드 솔루션 알고리즘을 개발하여 유지보수 계획 최적화에 기여합니다.

 

3. Problem description and formulation

Figure 1  The modeled maintenance planning problem

 

Table 2  The list of problem parameters

 

Table 3  The list of decision variables

 

The studied maintenance planning problem consists of (i) a set of assets that includes components/parts subject to fail, (ii) a maintenance facility divided into repair cells, (iii) repair cells with a different number of cross-trained maintenance workforce that has different skill sets, and (iv) a spare parts stock point where multiple types of repairable spare parts; i.e., stock keeping units (SKUs), are kept as inventory. Fig. 1 provides high-level visualization of the studied problem.

• 연구된 유지 보수 계획 문제는 (i) 고장이 발생할 수 있는 부품(parts)을 포함하는 자산 집합(set of assets), (ii) 수리 셀(repair cells)로 분할된 유지 보수 시설(maintenance facility), (iii) 서로 다른 기술 집합을 가진 교차 훈련된 유지 보수 인력의 수가 다른 수리 셀, (iv) 여러 유형의 수리 가능한 예비 부품, 즉 재고 보관 장치(SKU)가 재고로 보관되는 예비 부품 재고 지점(inventory)으로 구성됩니다. 그림 1은 연구된 문제의 높은 수준의 시각화를 제공합니다.

 

Tables 2 and 3 list the problem parameters and decision variables used to formulate the mathematical model, respectively. We introduce the remaining parameters when they are needed.

• 표 2와 표 3은 각각 수학적 모델을 공식화하는 데 사용된 문제 매개변수와 의사결정 변수를 나열한 것입니다. 우리는 필요할 때 나머지 매개변수를 소개합니다.

 

Problem Parameters (문제 매개변수)

• $N$: asset에 설치된 부품(SKU)의 종류 총 개수
• $\lambda_n$: 각 부품 종류 $n$의 고장율 (failure rate)
• $\mu_n$: 각 부품 종류 $n$의 수리율 (repair rate) (고장 시)
• $h_n$: 부품별 단위 시간당 유형별 예비 재고 보유 비용 (holding cost)
• $b$: 재고의 여유 부족으로 인하여 고장 부품을 다시 주문할 경우 단위 시간당 downtime 비용
• $\alpha$: 단위 시간당 유지보수 근로자(maintenance worker)에게 지급되는 기본급
• $\beta_n$: 부품 종류 $n$을 수리 가능한 노동자에게 지급되는 보상 금액 (일회성 훈련 비용 포함)

 

Decision Variables (결정 변수)

• $K$: 유지보수 시설(maintenance facility)의 총 수리 셀(repair cell) 개수
• $z_k$: 각 수리 셀(repair cell) $k$ 내 유지보수 인력(maintenance workers) 수
• $I_n$: 각 부품 종류 $n$ 별 예비 재고량 (기준 재고 수준)
• $x_{n,k}$: 각 부품 종류 $n$이 수리 셀 $k$에서 수리될 수 있는지 여부를 나타내는 이항 결정 변수 $k$ (결정 변수의 닫힌 형식 표현)
• $dd{I}$: 각 부품 종류 $n$별 재고 수준(spare inventory level)에 대한 closed-form 행 행렬 ($1 \times N$)
• ${X}$: 교차 훈련 정책(cross-training policy) (셀을 복구하기 위한 기술 할당)에 대한 closed-form 행렬 ($N\times K$), ${X}$의 요소 $(n, k)$는 이진 결정 변수 $x_{n,k}$에 대응함
• ${Z}$: 각 수리 셀 $k$의 유지보수 작업자 수($z_k$)에 대한 closed-form 행 행렬 ($1\times K$)

 

We assume that assets contain N distinct types of parts (SKUs), and each SKU is subject to random failure throughout its lifetime with a constant rate $λ_n(n=1,..., N )$. We assume that the failure rate of the part is independent of its age (i.e., how long it has been in use). Further, we model the failure behavior of SKUs with exponential probability distributions with parameter $λ_n (n = 1, . . . , N )$, which is a well-known assumption in repairable spare part inventory models (Sherbrooke 1968; Muckstadt 2005). We also assume the failure of an SKU is independent of other SKUs installed on the same asset.

• 저희는 자산이 $N$개의 서로 다른 유형의 부품(SKU)을 포함하고 각 SKU는 일정한 비율 $λ_n(n=1,..., N)$로 평생 동안 무작위 고장의 영향을 받는다고 가정합니다. 저희는 부품의 고장률이 수명(즉, 사용된 지 얼마나 되었는가)과 무관하다고 가정합니다. 또한 $λ_n(n = 1, ..., N)$ 매개변수를 사용하여 지수 확률 분포를 가진 SKU의 고장 동작을 모델링하며, 이는 복구 가능한 예비 부품 인벤토리 모델(Sherbrook 1968; Mukstadt 2005)에서 잘 알려진 가정입니다. 또한 SKU의 고장은 동일한 자산에 설치된 다른 SKU와 무관하다고 가정합니다.

 

When an in-use part fails, two things happen simultaneously: (i) an order is immediately placed for the same type of new (i.e., ready-for-use part) part to be supplied from spare stocks at the maintenance facility, and (ii) the failed part is sent to the maintenance facility as shown in Fig. 1.

• 사용중인 부품에 고장이 발생하면, (i) 정비시설의 예비재고로부터 공급받을 동일한 종류의 새 부품(즉, 사용 준비 부품)에 대해 즉시 주문을 하고, (ii) 고장이 발생한 부품은 그림 1과 같이 정비시설로 보내집니다.

 

The adopted spare inventory replenishment method mentioned in (i) corresponds to $( I_n − 1, I_n )$ policy. In this policy, the base stock inventory amount is equal to $I_n$ for SKU type $n (n = 1, . . . , N )$ and after each part failure, an order for a replacement is initiated for the same type of SKU. This is a well-known assumption used in repairable spare parts inventory systems (Sherbrooke 1986; Muckstadt 1973).

• (i)에 언급된 채택된 예비재고 보충방법은 $(I_n - 1, I_n )$ 정책에 해당합니다. 이 정책에서 기본재고량은 SKU type $n (n = 1, ..., N )$에 대해 $I_n$과 같으며, 각 부품고장 후 동일한 유형의 SKU에 대해 교체 주문이 시작됩니다. 이는 수리 가능한 예비부품 재고 시스템에서 사용되는 잘 알려진 가정입니다(Sherbrook 1986; Mukstadt 1973).

 

The failed part is shipped to the maintenance facility, and assigned to a repair cell $k (k = 1,..., K)$. We assume that each part type $n (n = 1,..., N)$ can be repaired at “only one" repair cell, and each repair cell $k$ should be able to repair at least one type of SKU. Further, we assume that each repair cell k contains cross-trained workers $z_k (\text{where } z_k ≥ 1)$ that can repair any type of SKU assigned to their repair cell.

• 고장난 부품은 유지 보수 시설로 배송되어 $k(k = 1,..., K)$ 복구 셀에 할당됩니다. 저희는 각 부품 유형 $n(n = 1,..., N)$은 "단 한 개" 복구 셀에서 복구할 수 있으며 각 복구 셀 $k$는 적어도 하나의 SKU 유형을 복구할 수 있어야 한다고 가정합니다. 또한 각 복구 셀 $k$에는 복구 셀에 할당된 모든 유형의 SKU를 복구할 수 있는 교차 훈련된 작업자 $z_k(\text{where } z_k ≥ 1)$가 포함되어 있다고 가정합니다.

 

The failed parts that can be repaired in cell $k$ form a single queue to be repaired by one of the maintenance workers in the cell (since all workforce in cell $k$ can repair all types of SKUs assigned to that cell). We use the first come first served (FCFS) queuing discipline (i.e., there is no priority between failed parts), and the first available worker in the cell repairs the failed part.

• 셀 $k$에서 수리할 수 있는 고장 부품은 셀의 유지 보수 작업자 중 한 명이 수리할 단일 대기열을 형성합니다(셀 $k$의 모든 인력이 해당 셀에 할당된 모든 유형의 SKU를 수리할 수 있기 때문). 저희는 선착순 서비스(FCFS) 대기열 규칙(즉, 고장 부품 사이에 우선 순위가 없음)을 사용하고 셀에서 사용 가능한 첫 번째 작업자가 고장 부품을 수리합니다.

 

The repair time of failed part type $n (n = 1, . . . , N )$ follows an exponential distribution with parameter $μ_n(n = 1, . . . , N )$. The exponential distribution is often applied to maintenance tasks where the repair completion times are independent of previous maintenance operations, and durations of repair operations have high variability Turan et al. (2020a). In the literature, it is also shown via simulation studies that the maintenance systems are often insensitive to the repair time distributions (Sleptchenko and van der Heijden 2016; Sleptchenko et al. 2018) We also assume that the repair time is independent of the maintenance worker who is performing the repair given that the worker has the skill to repair the part $n$.

• 고장 부품 유형 $n(n = 1, ..., N )$의 수리 시간은 매개 변수 $μ_n(n = 1, ..., N )$를 가진 지수 분포를 따릅니다. 지수 분포는 수리 완료 시간이 이전 유지 보수 작업과 무관하고 수리 작업 기간의 변동성이 높은 유지 보수 작업에 자주 적용됩니다. 또한 문헌에서 유지 보수 시스템이 종종 수리 시간 분포에 둔감하다는 것이 시뮬레이션 연구를 통해 나타났습니다(Sleptchenko and van der Heijden 2016; Sleptchenko et al. 2018). 또한 작업자가 파트 $n$을 수리할 수 있는 기술을 가지고 있기 때문에 수리 시간은 수리를 수행하는 유지 보수 작업자와 무관하다고 가정합니다.

 

The objective of the model is to minimize the total cost ${TC}$ by finding the (near) optimal settings of cross-training policy ${X}$, the number of maintenance workers to allocate each repair cell ${Z}$, and the number of spare stocks to keep in inventory for each part type ${I}$. The objective of the studied maintenance planning problem is given in Eq. (1).

• 모델의 목표는 교차 훈련 정책 ${X}$, 각 수리 셀 ${Z}$을 할당할 유지 보수 작업자의 수, 각 부품 유형 ${I}$에 대해 재고를 유지할 예비 재고 수를 찾아 총 비용 ${TC}$를 최소화하는 것입니다. 연구된 유지 보수 계획 문제의 목표는 식 (1)에 나와 있습니다.

 

Eq. (1)  유지보수 계획 문제의 목표함수와 수식

• $\min_{{X}, {Z}, {I}}$: ${X}$, ${Z}$, ${I}$에 대해 비용 Total Cost, $TC$를 최소화
• 제 1항 $\sum_n^N h_nI_n$: 부품별 단위 시간당 유형별 예비 재고 보유 비용 × 각 부품 종류 $n$ 별 예비 재고량 → 총 재고 보유 비용 (각 파트 $I_n$의 초기 재고 수준을 기반으로 계산)
• 제 2항 $\sum_k^K \alpha z_k$: 기본급 × 수리 셀 $k$의 유지보수 인력 수 → 기본급으로 노동력에 지급되는 비용
• 제 3항 $\sum_k^K z_k(\sum_n^N \beta_n x_{n,k})$: 각 셀 $k$의 유지보수 인력에 대하여 × (부품 $n$을 수리 가능한 경우 보상금액 × 파트 $n$이 수리 셀 $k$에서 수리 가능 여부)의 합 → 기본급 이외에 교차훈련된 노동력(한 가지 종류 이상의 부품 수리 가능)은 노동자가 보유한 기술 수에 따라 보상금을 받음
• 제 4항 $b\sum_n^N\mathbb{EBO}_n [{X}, {Z}, {I}_n]$: 고장 부품 재주문 시 단위 시간당 downtime 비용 × (SKU 종류 $n$에 대한 예상 백오더 수를 의사결정 변수 ${X}$, ${Z}$ 및 ${I}$의 함수로 계산)의 합 = backorder 단위 시간당 비용 × 총 backorder(중단된 asset) 수 → 총 backorder 비용 금액
• (*유지보수 시설의 예비 재고에서 고장 부품 교체 주문을 즉시 충족할 수 없는 경우 고장 부품에 대한 백오더 발생, 새 부품이 공급될 때까지 운용 자산이 감소)

 

The first summation term in Eq. (1) corresponds to the total inventory holding cost. This cost is calculated based on the initial stock levels for each part $I_n$, which is equal to the inventory position because of the implemented inventory replenishment method$(I_n −1,I_n)$ (Turan et al. 2018; Sleptchenko et al. 2019). The second cost term reflects the cost paid to the workforce as the base-level salary. In addition to the base-level salary, a cross-trained work- force (that has the ability to repair one or more types of failed parts) can get the compensation payment depending on the number of skills the worker has. The compensation payment also includes the one-time training cost for workers. The third summation term in the objective function captures these costs.

• 식 (1)의 제 1항은 총 재고 보유 비용에 해당함 이 비용은 각 파트 $I_n$의 초기 재고 수준을 기반으로 계산되며, 이는 시행된 재고 보충 방법으로 인해 재고 포지션과 동일합니다$(I_n -1, I_n)$
• 제 2항은 기본급으로 노동력에 지급되는 비용을 반영
• 제 3항은 기본급 외에 교차 훈련된 노동력(고장된 부품의 한 가지 이상의 유형을 수리할 수 있는 능력을 가진)은 노동자가 보유한 기술의 수에 따라 보상금을 받을 수 있음 보상금 지급에는 노동자의 일회성 훈련 비용도 포함

 

$(I_n - 1, I_n)$ Policy: This is a specific inventory replenishment policy where the base stock inventory level is set to $I_n$ for each SKU type $n$ (where n_n_ ranges from 1 to $N$). The notation $(I_n−1,I_n)$ indicates that when the inventory level drops to $I_n−1$, a replacement order is initiated. In other words, the system places an order for a new part when the stock of the specific SKU type reaches $I_n−1$.

• 기준 재고 수준을 $I_n$으로 설정한 특정한 재고 보충 정책
• 시스템은 부품 $n$에 대하여 재고 수준이 $I_n-1$로 하락하면 새로운 교체 부품 주문이 시작됨

 

When an order to replace the failed part can not be immediately met from the spare stocks at the maintenance facility, a backorder/backlog for the failed part occurs, and the asset goes down until a new part is supplied (either from the maintenance facility after the repair is completed or external part supplier). To reflect this, we calculate the “expected" number of backorders for SKU type $n$ denoted by $\mathbb{EBO}_n [·]$ as the function of decision variables ${X}$, ${Z}$, and ${I}$. The total number of backorders (the last summation term in objective function) represents the number of assets that are down, and we multiply this value by the downtime cost per unit time per part on backorder $b$ to obtain the total backorder cost (Turan et al. 2020c).

• 유지보수 시설의 예비 재고에서 고장 부품 교체 주문을 즉시 충족할 수 없는 경우 고장 부품에 대한 백오더/백로그가 발생하고 새 부품이 공급될 때까지 자산이 감소합니다(수리 완료 후 유지보수 시설 또는 외부 부품 공급업체에서). 이를 반영하기 위해 저희는 $\mathbb{EBO}_n[·]$로 표시되는 SKU 유형 $n$에 대한 "예상" 백오더 수를 의사결정 변수 ${X}$, ${Z}$ 및 ${I}$의 함수로 계산합니다. 총 백오더 수(목적 함수의 마지막 합산 항)는 중단된 자산 수를 나타내며, 이 값에 백오더 $b$의 단위 시간당 다운타임 비용을 곱하여 총 백오더 비용(Turan et al. 2020c)을 구합니다.

 

Constraints of some decision variables

The decision variables have to satisfy some constraints to be a feasible solution to the modeled problem.

• 결정 변수가 모델링된 문제에 대한 실현 가능한 해결책이 되려면 몇 가지 제약 조건을 충족해야 합니다.

 

First, the number of repair cells $K$ in the maintenance facility cannot be less than one or more than $N$ (in addition to being a positive integer $K ∈ \mathbb{Z}^+$). When the number of repair cells is equal to one, it is said that the maintenance facility is fully flexible/fully cross-trained, and in this type of facility each worker can fix all types of failures. In contrast, when the number of repair cells is equal to the number of distinct part types $N$ , it is called the facility is fully dedicated. That is, each worker can only repair one type of part.

• 첫째, 유지 보수 시설의 복구 셀 수 $K$는 1보다 작거나 $N$보다 클 수 없습니다 (양의 정수 $K ∈ \mathbb{Z}^+$, $1 \leq K \leq N$).
• 복구 셀의 수가 1개($K=1$)일 때, 유지 보수 시설은 완전히 유연하고 완전히 교차 훈련되며, 이러한 유형의 시설에서는 각 작업자가 모든 유형의 장애를 고칠 수 있다고 합니다.
• 대조적으로, 복구 셀의 수가 별개의 부품 유형 $N$의 수와 같을 때($K=N$), 이를 시설은 완전히 전용이라고 합니다. 즉, 각 작업자는 한 유형의 부품만 수리할 수 있습니다.

 

Eq. (2)  실현 가능한 교차훈련정책 ${X}$

Second, a feasible cross-training policy ${X}$ has to be a member of the set defined in Eq. (2). More specifically, each SKU type has to be repaired at exactly one repair cell and each repair cell should be able to repair at least one SKU type.

• 둘째, 실현 가능한 교차 훈련 정책 ${X}$는 식 (2)에 정의된 집합의 구성원이어야 합니다. 보다 구체적으로, 각 SKU 유형은 정확히 하나의 복구 셀에서 복구되어야 하며 각 복구 셀은 적어도 하나의 SKU 유형을 복구할 수 있어야 합니다.

 

Each repair cell $k$ has to contain at least one worker $(z_k ≥1, k =1,...,K)$ and $z_k \in \mathbb{Z}^+$. Further, it should be ensured that the utilization of each repair cell $k (k = 1, . . . , K )$ has to be less than one in order to prevent the number of failed parts waiting to be served in each cell to go infinity as time progress. To achieve this, a sufficient number of maintenance workers has to be allocated to repair cell $k$ in such a way that Eq. (3) holds.

• 각 리페어 셀 $k$에는 적어도 한 명의 작업자 $(z_k ≥1, k = 1, ..., K)$와 $z_k \in \mathbb{Z}^+$가 포함되어야 합니다. 또한 각 리페어 셀 $k(k = 1, ..., K)$의 활용도(utilization)가 1보다 작아야 시간이 진행됨에 따라 각 셀에서 제공되기를 기다리는 실패 부품의 수가 무한대가 되는 것을 방지할 수 있습니다. 이를 위해서는 식 (3)과 같이 충분한 수의 유지보수 작업자가 수리 셀 $k$에 할당되어야 합니다.

 

Lastly, the amount of spare inventory $I_n$ kept on stock for SKU type n has to be a non-negative integer $(I_n \in {0}∪\mathbb{Z}^+, n=1,...,N)$.

• 마지막으로 SKU 유형 $n$에 대해 재고로 남아 있는 예비 재고량($I_n$)은 음이 아닌 정수$(I_n \in {0} ∪\mathbb{Z}^+, n=1, ...,N)$여야 합니다.

 

The number of feasible cross-training policy ${X}$ that satisfies the set constraints in Eq. (2) for a given number of SKUs $N$ and the number of repair cells $K$ is the equivalent of the number of ways to partition a set of $N$ distinct objects into $K$ non-empty subsets.

• 주어진 수의 SKU $N$와 복구 셀 수 $K$에 대한 식 (2)의 설정 제약 조건(set constraints)을 충족하는 실현 가능한 교차 훈련 정책(feasible cross-training policy) ${X}$의 수는 $N$ 개의 별개 객체(distinct object) 집합을 $K$ 비공(non-empty) 부분 집합으로 분할하는 방법의 수와 동일합니다.

 

The latter is a well-known combinatorial problem with a solution equal to the Stirling number of the second kind (or Stirling partition number), which is denoted as $S(N, K)$ and calculated as follows:

• 후자는 Stirling number of the second kind (또는 스털링 파티션 번호)와 동일한 솔루션을 가진 잘 알려진 조합 문제로, $S(N, K)$로 표시되며 다음과 같이 계산됩니다:
• Stirling number of the second kind: $N$개의 서로 다른 객체를 $K$개의 비어 있지 않은 부분집합으로 나누는 경우의 수. 이 경우의 수는 $S(N, K)$로 표기되며, 동적 프로그래밍이나 재귀적인 방법을 사용하여 계산할 수 있습니다.
• Stirling numbers of the second kind

Stirling numbers of the second kind - Wikipedia

 

예를 들어, 13개의 객체를 6개의 부분집합으로 나누는 경우 ($N=13, K=6$)

 

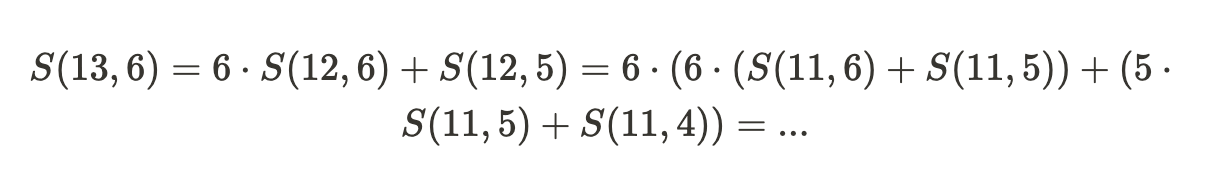
위와 같이 재귀와 memoization을 통해 효율적으로 계산이 가능함 (시간복잡도 $O(nk)$)

 

Since $K$ can take integer values between $1$ and $N$ , the exact total number of feasible cross-training policies $N C P ( N )$ can be calculated as the function of $N$ as follows:

• $K$는 $1$에서 $N$ 사이의 정수 값을 취할 수 있으므로 실현 가능한 교차 훈련 정책 $NCP(N)$의 정확한 총 수는 다음과 같이 $N$의 함수로 계산할 수 있습니다:

→ ($K$가 $1$부터 $N$일때 각각의 실현가능한 교차훈련정책의 개수)의 총합

 

Figure 2  $N$, $K$ 함수에 따른 실현 가능한 교차훈련정책 ${X}$ 개수의 변화 (log-scaled)

Figure 2 shows how $NCP(N)$ grows in the logarithmic scale, which proves the exponential increase in the size of decision space and the complexity of the problem. The size of the decision space gets even bigger when the decisions associated with the number of maintenance workers in each repair cell $z_k$ and the spare inventory levels for each SKU type $I_n$ are considered.

• 그림 2는 $NCP(N)$가 로그 스케일에서 어떻게 증가하는지 보여주며, 이는 결정 공간 크기의 기하급수적인 증가와 문제의 복잡성을 입증합니다. 각 수리 셀 $z_k$의 유지 보수 작업자 수와 각 SKU 유형 $I_n$의 예비 재고 수준과 관련된 결정을 고려할 때 결정 공간(decision space)의 크기는 더욱 커집니다.

 

Therefore, it is not possible or cumbersome to find the (near) optimal cross- training policy ${X}$ with traditional optimization methods or a brute-force enumeration. To mitigate this, we enhance an SA algorithm with DRL to systematically check the promising policies and efficiently search the mentioned decision space.

• 따라서 전통적인 최적화 방법이나 단순한 열거를 사용하여 (근접) 최적의 교차 훈련 정책 ${X}$을 찾을 수 없거나 번거롭습니다. 이를 완화하기 위해 DRL을 사용한 SA 알고리즘을 향상시켜 유망한 정책을 체계적으로 확인하고 언급된 결정 공간을 효율적으로 검색합니다.

 

4. Solution approach

In this section, we discuss the details of the solution approach. The approach basically contains three subroutines: (i) a Simulated Annealing (SA) meta-heuristic, (ii) a Double Deep Q-Network-based Deep Reinforcement Learning (DRL) algorithm, and (iii) a simple greedy heuristic that uses a queuing approximation.

• 이 섹션에서는 솔루션 접근 방식의 세부 사항에 대해 논의합니다. 이 접근 방식에는 기본적으로 (i) SA 메타 휴리스틱, (ii) DDQN 기반 DRL 알고리즘, (iii) queuing 근사를 사용하는 간단한 그리디 휴리스틱의 세 가지 하위 루틴이 포함되어 있습니다.

 

These subroutines work collaboratively and iteratively to seek (near) optimal solutions for cross-training policy ${X}$, the number of maintenance workers to allocate each repair cell ${Z}$, and the number of spare stocks to keep in inventory for each part type ${I}$ as shown in Fig. 3.

• 이러한 하위 루틴은 협력적이고 반복적으로 작동하여 교차 훈련 정책(cross-training policy) ${X}$, 각 복구 셀 ${Z}$을 할당할 유지 보수 작업자 수, 그림 3과 같이 각 부품 유형 ${I}$에 대해 인벤토리에 유지할 예비 재고(spare stocks) 수를 찾습니다.

 

Figure 4  5개의 SKU와 2개의 수리 셀(repair cells)로 구성된 유지보수 시설(maintenance facility)에 대한 예시 솔루션 표현 ($N=5, K=2$)

We use a one-dimensional array encoding scheme to represent the solutions as shown in Fig. 4. The first part of the array shows the cross-training policy ${X}$. The length of this part (i.e., the number of cells) is equal to the number of part types (SKUs) $N$ in the model. For the illustrative representation in Fig. 4, we have five SKUs in the model. For this part of the array, the number in each cell indicates the assignments of SKUs to repair cells. In the example, SKU 1, 2, and 5 are assigned to repair cell 1.

• 저희는 그림 4와 같은 솔루션을 나타내기 위해 1차원 어레이 인코딩 방식을 사용합니다. 어레이의 첫 번째 부분은 교차 훈련 정책 ${X}$을 보여줍니다. 이 부분의 길이(즉, 셀 수)는 모델의 부품 유형 수(SKU) $N$와 동일합니다. 그림 4의 예시적인 표현을 위해 모델에 5개의 SKU가 있습니다. 어레이의 이 부분의 경우 각 셀의 숫자는 SKU의 수리 셀로의 할당을 나타냅니다. 예제에서 SKU 1, 2 및 5는 수리 셀 1에 할당됩니다.

 

The second part of the array corresponds to the number of maintenance workers allocated to each repair cell ${Z}$. The length of this part (i.e., the number of cells) is dynamic and varies depending on the distinct numbers used in the first part of the array. In the example, the number of repair cells in maintenance facility $K$ is two, and the first repair cell contains two and the second repair cell contains three workers.

• array의 두 번째 부분은 각 수리 셀 ${Z}$에 할당된 유지보수 작업자 수($z_k$)에 해당합니다. 이 부분의 길이(즉, 셀 수)는 동적이며 어레이의 첫 번째 부분에 사용된 고유한 숫자에 따라 달라집니다. 예제에서 유지보수 설비 $K$의 리페어 셀 수는 2개이고, 첫 번째 리페어 셀은 2개, 두 번째 리페어 셀은 3개의 작업자를 포함합니다.

 

Eq. (4)  위 예시에 따른 각각의 행렬 ${X}$, ${Z}$, ${I}$의 예시

The last part of the array represents the number of spare stocks to keep in inventory for each part type ${I}$, and the length of this part is again equal to the number of part types (SKUs) $N$ . The number in each cell denotes how many spares should be kept on stock for that SKU type. For example, for SKUs 1 and 5, it is not required to keep any spare stocks; i.e., $I_1 = I_5 = 0$. Solutions corresponding to Fig. 4 are shown in Eq. (4).

• array의 마지막 부분은 각 부품 유형 ${I}$의 재고에 보관해야 하는 예비 재고 수를 나타내며, 이 부분의 길이는 다시 부품 유형(SKUs) $N$의 수와 동일합니다. 각 셀의 숫자는 해당 SKU 유형에 대해 재고에 보관해야 하는 예비 재고 수를 나타냅니다. 예를 들어, SKU 1과 5의 경우 $I_1 = I_5 = 0$의 예비 재고를 유지할 필요가 없습니다. 그림 4에 해당하는 솔루션은 식 (4)에 나와 있습니다.
• 각 행렬의 차원은 다음과 같음
  • ${X}$ : $N × K$ (이때, 각 row는 one-hot encoded)
  • ${Z}$ : $1 × K$
  • ${I}$ : $1 × N$

 

In the remainder of this section, we first discuss the key components of the reinforcement learning algorithm in Sect. 4.1. Section 4.2 explains why deep reinforcement learning is used. In Sect. 4.3, we give the details of the SA algorithm used, and in Sect. 4.4 we describe how we combined the ideas in DRL and SA. In Sect. 4.5, we discuss details of the greed heuristic that optimizes ${Z}$ and ${I}$. Lastly, in Sect. 4.6, we list the value of all parameters that we used throughout the solution approach.

• 이 섹션의 나머지 부분에서는 먼저 섹션 4.1의 강화 학습 알고리즘의 주요 구성 요소에 대해 설명합니다. 섹션 4.2에서는 심층 강화 학습이 사용되는 이유에 대해 설명합니다. 섹션 4.3에서는 사용된 SA 알고리즘에 대해 자세히 설명하고, 섹션 4.4에서는 DRL과 SA에서 아이디어를 결합한 방법을 설명합니다. 섹션 4.5에서는 ${Z}$ 및 ${I}$를 최적화하는 탐욕 휴리스틱에 대해 자세히 설명합니다. 마지막으로 섹션 4.6에서는 솔루션 접근 방식 전반에 걸쳐 사용한 모든 매개 변수의 값을 나열합니다.

 

4.1. Reinforcement Learning (RL)

Reinforcement learning (RL) is a type of machine learning technique concerning how intelligent agents should take actions in an environment to maximize the cumulative reward (Hu et al. 2020). In a basic reinforcement algorithm, a decision-maker (also called an agent) is located in environment $E$. The agent sequentially interacts with the environment over time. At time step $t$, the agent gets the representation of the environment, which is called a state and denoted as $s_t ∈ S$, where $S$ is the set of all possible states. Observing the state $s_t$ , the agent chooses an action denoted as $a_t ∈ A$ to take under a policy $\pi$, where $A$ denotes the set of all possible actions. Once the agent takes the action at, it gets a reward $r_{t+1}$ and the environment transitions to a new state $s_{t+1}$. The goal of the agent under the policy $\pi$ is to maximize its expected return $G$, while trying to reach its goal state as formulated in Eq. (5).

• 강화 학습(RL)은 지능형 에이전트가 누적 보상을 최대화하기 위해 환경에서 어떻게 조치를 취해야 하는지에 관한 기계 학습 기술의 한 유형입니다(Hu et al. 2020). 기본 RL 알고리즘에서 의사 결정자(agent)는 Environment $E$에 위치합니다. 에이전트는 시간이 지남에 따라 순차적으로 환경과 상호 작용합니다. Time step $t$에서 에이전트는 환경의 representation을 가져오며, 이 표현을 state라고 하고 $s_t ∈ S$로 표시하며, 여기서 $S$는 모든 가능한 상태의 집합입니다. State $s_t$를 관찰하면 에이전트는 $a_t ∈ A$로 표시된 action을 선택하여 Policy $\pi$에서 수행합니다. 에이전트가 action을 수행하면 보상 $r_{t+1}$을 받고 환경은 새로운 상태 $s_{t+1}$로 전환됩니다. 정책 $\pi$에 따른 에이전트의 목표는 식 (5)에 공식화된 목표 상태에 도달하려고 노력하면서 예상 수익(Expected Return) $G$를 최대화하는 것입니다.

 

Eq. (5)  RL에서 Expected Return $G_t^\pi$

where $\Tau$ is the number of steps to take to reach the goal state from $s_t$ and $γ$ is the discount factor whose value is between $[0, 1]$ indicating how much to discount future rewards. Lower values of $γ$ significantly discount the future rewards while a value of 1 gives equal importance to all future rewards.

• 여기서 $\Tau$는 $s_t$에서 목표 상태에 도달하기 위해 취해야 할 단계 수이고 $γ$는 $[0, 1]$ 사이의 값으로 미래 보상을 얼마나 할인(discount)해야 하는지 나타내는 discount factor입니다. $γ$의 값이 낮으면 미래 보상이 크게 할인되는 반면 1의 값은 모든 미래 보상에 동등한 중요성을 부여합니다.

 

4.2. Deep Reinforcement Learning (DRL)

Deep reinforcement learning is the combination of reinforcement learning (RL) and deep learning. The term deep learning implies that an artificial neural network structure with more than 1 hidden layer is used while performing learning.

• Deep Reinforcement Learning은 RL과 딥러닝의 결합입니다. 딥러닝이라는 용어는 학습을 수행하는 동안 하나 이상의 은닉 계층을 가진 인공 신경망(ANN) 구조가 사용된다는 것을 의미합니다.

 

Unfortunately, RL exhibits several limitations in practice when deployed in high-dimensional and complex stochastic domains, mainly manifesting algorithmic instabilities with solutions that significantly diverge from optimal regions, or exhibiting slow value updates at infrequently visited states (Andriotis and Papakonstantinou 2018). In such scenarios, deep learning methods are incorporated to solve the problem.

• 안타깝게도 RL은 주로 최적의 영역에서 크게 벗어나는 솔루션으로 알고리즘 불안정성을 나타내거나 자주 방문하지 않는 상태에서 느린 값 업데이트를 나타내면서 고차원적이고 복잡한 확률적 도메인에 배치될 때 실제로 몇 가지 한계를 나타냅니다(Andriotis and Papakonstantinou 2018). 이러한 시나리오에서는 문제를 해결하기 위해 딥러닝 방법이 통합됩니다.

 

The deep neural networks are strong function approximators. To benefit from their approximation capabilities in the reinforcement learning area, especially when the state-action space is very complex, they are used as policy function approximators as in Huang et al. (2020).

• DNN은 강력한 함수 추정기(function approximators)입니다. 특히 State-Action Space가 매우 복잡한 경우 RL 영역에서 근사 기능의 이점을 얻기 위해 Huang et al. (2020)에서와 같이 정책 함수(Policy function) 추정기로 사용됩니다.

 

4.3. Simulated Annealing (SA)

Simulated annealing algorithm is initially introduced by Kirkpatrick (1984) which is one of the most popular and robust meta-heuristic algorithms that enable us to solve many hard combinatorial optimization problems (Suman and Kumar 2006) such as The Traveling Salesman Problem (TSP) (Kirkpatrick et al. 1983), and Quadratic Assignment Problem (QAP)(Connolly 1990).

• Simulated Annealing (담금질 기법) 알고리즘은 여행 세일즈맨 문제(TSP)(Kirkpatrick et al. 1983) 및 4차 할당 문제(QAP)(Connolly 1990)와 같은 많은 어려운 조합 최적화 문제(Suman and Kumar 2006)를 해결할 수 있는 가장 인기 있고 강력한 메타 휴리스틱 알고리즘 중 하나로, Kirkpatrick(1984)에 의해 처음 도입되었습니다.
• 메타 휴리스틱(meta-heuristic)은 problem에 independent하여 대부분의 문제에 적용이 가능하고, 보다 general한 휴리스틱 알고리즘을 말함 따라서 더 고도의 알고리즘이 요구됨

 

The SA uses a stochastic approach to avoid local optimum traps. In particular, SA searches for possible neighborhood solutions allowing a move to the neighboring solution even if the moved neighbor result is worse than the current one. In an analogy of SA with an optimization procedure, the physical material states correspond to problem solutions, the energy of a state to the cost of a solution, and the temperature to a control parameter (Du and Swamy 2016).

• SA는 local optima 함정을 피하기 위해 확률적 접근 방식을 사용합니다. 특히 SA는 이동된 이웃 결과(neighbor result)가 현재보다 좋지 않더라도 이웃 솔루션(neighboring solution)으로 이동할 수 있는 가능한 이웃 솔루션을 검색합니다.
• 최적화 절차와 SA의 유사한 점 (correspond to) (Du and Swamy 2016).
  • 물리적 물질 상태 → 문제 solution(해)
  • state의 energy → cost of a solution
  • 온도(temperature) → 제어 매개변수 (a control parameter)
  • Simulated annealing

Simulated annealing - Wikipedia

 

The flowchart of the algorithm details can be found in the SA part of Fig. 3 which is highlighted in red. The algorithm starts with an initial feasible solution.

At each iteration, SA generates a neighborhood solution and determines the objective function value based on this solution. If the resulting solution is better than the current solution then the new solution is accepted unconditionally. Otherwise, the neighborhood solution is accepted with the probability of $e^{(−\Delta E/T)}$ where $T$ denotes the current temperature and $\Delta E$ denotes the difference between objective functions of current and the neighborhood solutions.

• 알고리즘 세부 사항의 흐름도는 그림 3의 SA 부분에서 확인할 수 있으며 빨간색으로 강조되어 있습니다. 알고리즘은 초기 실현 가능한 솔루션(initial feasible solution)으로 시작합니다. 각 반복에서 SA는 이웃 솔루션(neighborhood solution)을 생성하고 이 솔루션을 기반으로 목적 함수 값(objective function value)을 결정합니다.
• 결과 솔루션이 현재 솔루션보다 나은 경우 새로운 솔루션을 무조건 수락합니다. ($\Delta E \leq 0$)
• 그렇지 않으면 $T$는 현재 온도를 나타내고 $\Delta E$는 현재와 이웃 솔루션의 목적 함수 간의 차이를 나타내는 $e^{(-\Delta E/T)}$의 확률로 이웃 솔루션을 수락합니다. ($T$가 가장 작은 Global Optima를 찾는 것이 목표)
• 예를 들어, 현재 솔루션이 10℃, 이웃 솔루션이 15℃라면 $T=10$, $\Delta E = 15 - 10=5$이다. 따라서 이웃 솔루션을 수락할 확률은 $e^{-\Delta E /T}=e^{-5/10}=e^{-0.5}=0.6065...$이다.
• 아래는 $\Delta E$에 따른 확률 비교 표이다. ($T=10$)

$\Delta E$가 0에 가까울수록 수락 확률은 1에 가까워지고, $\infin$에 가까울수록 수락 확률은 0에 수렴함

함수가 $e^{-x}$꼴이므로, 0에 가까울수록 1에 수렴하고, $\infin$으로 발산할수록 0에 수렴하는 모양

 

Thus, the probability of accepting a worse solution is larger at high temperatures. The parameter of the temperature has crucial importance in the SA procedure since the acceptance probability is controlled with the temperature. This parameter gradually decreases at each iteration. Therefore, the probability of accepting uphill moves (accepting worse solution) is large at high $T$, and is low at low $T$.

• 따라서 더 나쁜 솔루션(worse solution)을 수락할 확률은 고온에서 더 큽니다. 온도의 매개변수는 수락 확률이 온도로 제어되기 때문에 SA 절차에서 결정적인 중요성을 갖습니다. 이 매개변수는 반복할 때마다 점차 감소합니다. 따라서 오르막 이동을 수락(더 나쁜 솔루션을 수락)할 확률은 높은 $T$에서 크고 낮은 $T$에서 낮습니다.
• 애초에 현재 온도인 $T$가 높다면 (고온이라면) 상대적으로 고온인 worse solution을 수락할 확률이 큼
  • 위 비교표를 보면 $\Delta E$가 같더라도 $T$가 높으면 더 나쁜 해의 선택 확률이 큼 ($\Delta E=10$ 주황 표 참고)
  • 선택된 더 나쁜 해(worse neighbor solution)의 값이 같더라도 현재 $T$가 높으면 더 나쁜 해의 선택 확률이 더 크다 (노란 표 참고)

 

4.4. DRLSA

Our algorithm, denoted as DRLSA, is a combination of Deep Reinforcement Learning (DRL) and Simulated Annealing (SA) algorithms.

• DRLSA로 표시되는 우리의 알고리즘은 DRL과 SA 알고리즘의 조합임

 

4.4.1. State Space

In the DRLSA, a state $s_t$ represents the cross-training policy ${X}$ mentioned in Sect. 3 and the finite state space $S$ is any representation that ${X}$ can get.

• DRLSA에서 상태 $s_t$는 섹션 3에서 언급된 교차 훈련 정책 ${X}$를 나타내며 유한 상태 공간 $S$는 ${X}$가 얻을 수 있는 모든 표현입니다. (${X}$의 차원은 $N × K$)

 

4.4.2. Action Space

The finite action space $A$ is composed of the following three actions. The first action $a^1$, selects two random positions in the solution vector and swaps elements of these positions. The second action $a^2$, selects one element of the solution vector randomly and changes the value of this element. Similarly, the third action $a^3$, selects two elements of the solution vector randomly and changes the value of these elements. ($a^1, a^2, a^3 \in A$)

• 유한한 action space $A$는 다음 세 가지 action으로 구성됩니다. $n(A)=3$ (cardinality가 $3$)
  • 첫 번째 action $a^1$는 해 벡터에서 두 개의 임의의 위치를 선택하고 이 위치의 원소를 swap합니다.
  • 두 번째 작용 $a^2$는 해 벡터의 한 원소를 임의로 선택하고 이 원소의 값을 변경합니다.
  • 세 번째 작용 $a^3$는 해 벡터의 두 원소를 임의로 선택하고 이 원소의 값을 변경합니다. ($a^2$와 유사)

 

4.3. Follow of the approach

In our implementation of the algorithm, both DRL and SA benefit from each other’s feedback, as shown in Fig. 3. The DRL starts with a random initial state $s_0$ and runs for a number of time steps, tries to learn which actions to take depending on the current state by changing its internal parameters, and passes the best state $s_{\text{best}}$ it encounters during its training to SA. The SA then uses $s_{\text{best}}$ as its initial solution, runs for several iterations and passes back its best solution $s_{\text{best}}$ to DRL, and thus one episode becomes completed. The combined algorithm runs for a number of episodes, and the final $s_{\text{best}}$ value, and its corresponding cost are reported as the final solution. The pseudo-code of the algorithm can be found in Algorithm 1 which in itself calls Algorithm 2.

• 우리의 알고리즘 구현에서 DRL과 SA는 그림 3과 같이 서로의 피드백을 통해 이점을 얻습니다. DRL은 무작위 초기 상태 $s_0$로 시작하여 여러 step들을 실행하고 내부 매개 변수를 변경하여 현재 상태에 따라 수행해야 할 작업을 학습하고 훈련 중에 발생하는 최고의 state인 $s_{\text{best}}$를 SA에 전달합니다. 그런 다음 SA는 $s_{\text{best}}$를 초기 솔루션으로 사용하고 여러 번 반복하여 실행하며 최고의 솔루션 $s_{\text{best}}$를 DRL에 다시 전달하므로 한 에피소드가 완료됩니다. 결합된 알고리즘은 여러 에피소드 동안 실행되며 최종 $s_{\text{best}}$ 값과 해당 비용이 최종 솔루션으로 보고됩니다. 알고리즘의 의사 코드는 Algorithm 1에서 함수 DRLSA(s0, obj, batch_size, gamma)를 찾을 수 있으며, Algorithm 1에서 Algorithm 2인 SA(obj, RB)를 호출함

 

Algorithm 1  DRL Backed SA Algorithm (DRLSA)

 

Algorithm 2  Simulated Annealing Algorithm (SA)

 

4.4.4 Double Deep Q-Network

The type of the RL algorithm we used is Q-Learning (Watkins and Dayan 1992). Q-learning aims at learning the optimal action-value functions (also known as the Q-value functions or Q-functions) to derive the optimal maintenance management policy (Mahmoodzadeh et al. 2020). A Q-value, $Q(s_t , a_t)$ denotes how good it is to take the action at from state $s_t$. Traditional Q-learning uses a tabular structure(Q-table) to learn how to map action-state pairs to Q-values. Because of the complexity of the action-state space in our problem, using a Q-table-based solution wouldn’t be feasible. Therefore, we adopted the Double Deep Q- Network described in Huang et al. (2020) which is derived from the basic deep Q-Network by Mnih et al. (2015) to approximate the Q-function. As depicted in Fig. 5, the first deep Q-network, denoted as $D Q N$ and is used as a policy network, takes a state $s_t$ as input and produces Q-values for each possible action. The optimal Q-function $Q^{*}$ is formulated as in Eq. (6) which uses the Bellman optimality equation as an iterative update process to estimate the optimal Q-value for a given state-action pair $(s_t , a_t )$.

• 저희가 사용한 RL 알고리즘의 유형은 Q-Learning(Watkins and Dayan 1992)입니다. Q-Learning은 최적의 유지 보수 관리 정책(Mahmoodzadeh et al. 2020)을 도출하기 위해 최적의 action-value (행동 가치) 함수(Q-value 함수 또는 Q-함수라고도 함)를 학습하는 것을 목표로 합니다. Q-value인 $Q(s_t, a_t)$는 상태 $s_t$에서 작업을 수행하는 것이 얼마나 좋은지 나타냅니다. (어떠한 state에서 어떠한 action의 가치) 기존의 Q-러닝은 action-state 쌍을 Q-값에 매핑하는 방법을 학습하기 위해 표 구조(Q-table)를 사용합니다. 문제의 action-state space가 복잡하기 때문에 Q-테이블 기반 솔루션을 사용하는 것은 불가능합니다. 따라서 저희는 Q-함수를 근사화하기 위해 Mnih et al.(2015)에 의해 기본 Deep Q-Network에서 파생된 Huang et al.(2020)에 설명된 Double Deep Q-Network (DDQN)를 채택했습니다. 그림 5와 같이 $D Q N$로 표시되고 정책 네트워크로 사용되는 첫 번째 DQN는 상태 $s_t$를 입력으로 가져와 가능한 각 action에 대한 Q-value를 생성합니다. 최적의 Q-함수 $Q^{*}$는 주어진 state-action 쌍 $(s_t, a_t)$에 대한 최적의 Q-값을 추정하기 위해 반복 업데이트 프로세스로 Bellman Optimality Equation을 사용하는 식 (6)과 같이 공식화됩니다.

 

 

Reward of DRLSA

The equation states that for a given state-action pair $(s_t , a_t )$ at time $t$ , the expected return of starting from state $s_t$, selecting action at and following the optimal policy thereafter will be the expected reward $r_{t+1}$, we get from taking action $a_t$ in state $s_t$ plus the maximum expected discounted return that can be achieved from any possible next state-action pairs $(s_{t+1},a_{t+1})$.

• 이 방정식은 시간 $t$에서 주어진 state-action 쌍 $(s_t, a_t)$에 대해 상태 $s_t$에서 시작하여 최적의 정책에서 action을 선택하고 그 이후에 수행하는 expected reward은 $r_{t+1}$이며, state $s_t$에서 action $a_t$에 가능한 다음 state-action 쌍$(s_{t+1}, a_{t+1})$에서 달성할 수 있는 최대 expected discounted return을 더한 것입니다.

 

The reward value $r_{t+1}$ for DRLSA is defined as the difference between the total cost of the current state $obj(s_t)$, and the total cost of the next state $obj(s_{t+1})$. If the following state yields a lower cost value than the current state, the reward will be positive.

• DRLSA에 대한 reward 값 $r_{t+1}$은 현재 state $obj(s_t)$의 총 cost와 다음 state $obj(s_{t+1})$의 총 cost의 차이로 정의됩니다. 다음 상태가 현재 상태보다 낮은 비용 값을 산출하면 보상은 양수가 됩니다.

 

Epsilon-Greedy Strategy

While selecting an action (selectAction() in Algorithm 1) we use Epsilon($ε$)-greedy strategy.

• Algorithm 1에서 action selectAction()을 선택하는 동안 저희는 Epsilon( $ε$)-greedy 전략을 사용

 

The exploration rate $ε$ is initially set to 1, which means the agent will explore the environment rather than exploit it. As the agent learns more about the environment, $ε$ gets decayed exponentially by some factor and the agent explores the environment with probability $ε$, and exploits it with probability $1 − ε$. Exploring the environment corresponds to choosing a random action while exploiting it means selecting the best action with maximum Q-Value, obtained by using $DQN$ . We use a second Q-network called the target network, denoted as $DQN_{target}$, to calculate $Q^*(s_{t+1},a_{t+1})$ part of Eq. (6). This type of architecture is called Double Deep Q-Network ( $D D Q N$ ) and leads to less overestimation of the Q-learning values, as well as improved stability, and hence improved performance (Hu et al. 2020).

• 탐색 속도 $ε$는 처음에 1로 설정되며, 이는 에이전트가 환경을 사용하는 것이 아니라 환경을 탐색한다는 것을 의미합니다. 에이전트가 환경에 대해 더 많이 알게 되면 $ε$는 어떤 요인에 의해 기하급수적으로 붕괴(감소)되고 에이전트는 $ε$의 확률로 환경을 탐색(explore)하여 $1 - ε$의 확률로 환경을 활용(exploit)합니다. 환경을 탐색하는 것은 $DQN$을 사용하여 얻은 최대 Q-Value로 최적의 action을 선택하는 것을 의미합니다. 저희는 $DQN_{target}$로 표시되는 Target Network라는 두 번째 Q-Network를 사용하여 $Q^*(s_{t+1}, a_{t+1})$를 계산합니다. 이러한 유형의 아키텍처를 Double Deep Q-Network($DDQN$)라고 하며 Q-러닝 값의 과대평가(overestimation)를 줄일 뿐만 아니라 안정성(stability)을 향상시켜 성능을 향상시킵니다 (Hu et al. 2020).

 

Figure 5  $L$개의 은닉층, $D$개 입력부와 $C$개의 출력부가 있는 DQN, 여기서 $C$는 가능한 action의 수 $n(A)$를 나타냄.

 $l$번째 은닉층은 $h(l)$개의 은닉층을 포함한다. State 상태 $s_t$는 네트워크에 입력(input)으로 들어가고, 각 action인 $a^i$인 $Q(s_t, a^i)$의 Q-Value는 예측값으로 출력(output)됨

 

Optimal Q-Value (by DQN Target Network)

The structure of $DQN_{target}$ is the same as $DQN$, and they share the same parameters at first. The only difference is that during training, the parameters of $DQN_{target}$ are not updated for a predefined number of episodes, $η$, while the parameters of t$he D Q N$ are being updated at each iteration. After $η$ episodes, the parameters of $DQN_{target}$ are set to have the parameter values of the $D Q N$ . Equation (7) reformulates the optimal Q-Value in terms of networks.

• $DQN_{target}$의 구조는 $DQN$와 동일하며 처음에는 동일한 매개변수를 공유합니다. 유일한 차이점은 훈련 중에 $DQN_{target}$의 매개변수는 미리 정의된 에피소드 수 $η$에 대해 업데이트되지 않는 반면, $DQN_{target}$의 매개변수는 각 반복에서 업데이트되고 있다는 것입니다. $η$ 에피소드 후 $DQN_{target}$의 매개변수는 $DQ N$의 매개변수 값을 갖도록 설정됩니다. 식 (7)은 네트워크 측면에서 최적의 Q-Value를 재구성합니다.

Eq. (7)  DQN의 Target Network를 통해 최적 Q-value $Q^*$를 계산하는 식

 

Loss of DQN Networks

Since the Q-values produced by the network are real-valued numbers, the Mean Squared Error(MSE) loss function is used to train the network. It finds the error between the approximated optimal Q-value, $Q^*(s_t , a_t )$, and the Q-value of the current state-action pair, $Q(s_t , a_t )$ as formulated in Eq. (8).

• Network에서 생성된 Q Value는 실제 값을 갖는 숫자이므로 평균 제곱 오차(MSE) 손실 함수를 사용하여 네트워크를 학습(train)합니다. 근사적인 최적(optimal) Q-value $Q^*(s_t, a_t)$와 현재 state-action 쌍의 Q-value $Q(s_t, a_t)$ 사이의 오차를 식 (8)에 공식화했습니다.

Eq. (8)  최적 Q-value $Q^*$와 현재 Q-value의 오차값 $L$

 

Experience Replay Buffer ($RB$)

To break the sequential behavior of the learning algorithm, we incorporated Experience Replay technique which was proved to improve the performance of the Q-networks. After each action is taken, the state, action, reward, and the next state value quadruple $(s_t,a_t,r_{t+1},s_{t+1})$, called experience and denoted as $ξ$ is stored in a queue named Replay Buffer($RB$). During each episode, both DRL and SA populate the $RB$ with their experiences. At each iteration of the network training, if there are enough samples in the buffer, a number of experiences are sampled from $R B$ and are fed as input to the network to optimize the parameters of $D Q N$ .

The two important feedbacks that DRL gets from SA are the next state values and the experiences. Every time SA makes an iteration, it stores its experience $ξ$ in DRL’s $R B$ so that DRL can use those experiences as a guide to update its parameters and learn how to predict which actions to take in upcoming episodes.

• 학습 알고리즘의 순차적인 동작을 중단(break)하기 위해 Q-Network의 성능을 향상시키는 것으로 입증된 Experience Replay 기술을 통합했습니다. 각 작업이 수행된 후 state, action, reward 및 next state 값 $(s_t,a_t,r_{t+1},s_{t+1})$가 경험이라고 하고 $ξ$로 표시되는 Experience Replay Buffer($RB$)라는 큐에 저장됩니다. 각 에피소드 동안 DRL과 SA는 모두 경험으로 $RB$를 채웁니다. 네트워크 학습을 반복할 때마다 버퍼에 충분한 샘플이 있는 경우 여러 경험이 $RB$에서 샘플링되고 $D Q N$의 매개 변수를 최적화하기 위한 네트워크 입력으로 제공됩니다.
• DRL이 SA로부터 얻는 두 가지 중요한 피드백은 next state value과 experience(경험)입니다. SA는 반복을 수행할 때마다 경험 $ξ$를 DRL의 $RB$에 저장하여 DRL이 이러한 경험을 지침으로 사용하여 매개 변수를 업데이트하고 향후 에피소드에서 어떤 조치를 취해야 할지 예측하는 방법을 배울 수 있습니다.

 

4.5. Optimizing workforce and spare part inventories for repair cells

We use a simple greedy heuristic to find the optimal values of workers to allocate each repair cell $z_k (k = 1, . . . , K )$ and base stock inventory levels $I_n$ for each SKU type $n (n = 1, . . . , N )$ for a given cross-training policy ${X}$ produced by DRLSA as shown in Fig. 3.

• 간단한 greedy 휴리스틱을 사용하여 그림 3과 같이 DRLSA에서 생성한 주어진 교차 훈련 정책 ${X}$에 대해 각 수리 셀에 할당되는 작업자의 수 $z_k(k = 1, ..., K)$ 및 기본 재고 수준 $I_n$들의 최적 값을 찾습니다.

 

The greedy heuristic consists of two collaboratively acting subroutines. At the initial step, the workforce optimizer subroutine allocates the minimum number of workers required to each repair cell $k$ by using which ensures the feasibility of Eq. (3).

• Greedy 휴리스틱은 협력적(collaboratively)으로 행동하는 두 개의 서브루틴(subroutines)으로 구성됩니다. 첫 단계에서 작업자 최적화 서브루틴(workforce optimizer subroutine)은 다음을 사용하여 각 복구 셀 $k$에 필요한 최소 작업자 수 $z_k$를 할당합니다, 식 (3)의 실현 가능성을 보장합니다.

Eq. (9) $z_k$를 greedy heuristic을 통해 계산

 

$x_{n,k}$ : 부품 종류 $n$이 수리 셀 $k$에서 수리 가능 여부 × ($\lambda_n$ : 부품 종류 $n$의 고장률 failure rate / $\mu_n$ : 부품 종류 $n$ 고장 시 수리율 repair rate) → 수리 가능 여부 × (고장률 / 수리율)

정수일 경우 → 비둘기집 원리에 따라 정수 $+ 1$한 값을 $z_k$로 채용

소수일 경우 → 가우스 괄호: $⌈x⌉=min{n∈Z:n≥x}$ ($x$ 이상의 정수 중 가장 작은 정수, 즉 올림)

Since repair cells are independent of each other based on the discussion provided by Turan et al. (2020b), Sleptchenko et al. (2019), we treat each repair cell $k$ as a Markovian (due to exponential probability distributions for failure and service times) multi-class multi-server queuing systems $M/M/z_k$ where servers correspond to maintenance workers in repair cell $k$ and classes correspond the set of SKU types that are assigned to cell $k$.

• Turan et al. (2020b), Sleptencho et al. (2019)에서 제공하는 논의를 기반으로 수리 셀(repair cells)은 서로 독립적이기 때문에 각 수리 셀 $k$를 Markov 시스템(고장 및 서비스 시간에 대한 지수 확률 분포로 인해) 다중 클래스 다중 서버 큐잉 시스템 $M/M/z_k$로 취급하며, 여기서 서버는 복구 셀 $k$의 유지 보수 작업자에 해당하고 클래스는 셀 $k$에 할당된 SKU 유형 집합에 해당합니다.
• $M/M/z_k$는 큐잉(대기) 이론의 영역에서 큐잉 시스템을 의미
• $M/M$: 메모리가 없는 도착과 지수 서비스 시간(Stands for memoryless arrivals and exponential service times)을 의미합니다. 이 맥락에서 entity(일반적인 의미에서 고객)의 도착은 포아송 프로세스를 따르고 서비스 시간은 지수적으로 분포되어 있음을 의미 (service times are exponentially distributed)함
• $z_k$: 시스템에 있는 서버의 수를 나타냅니다. 특히 repair cell $k$에서 유지보수 작업자를 나타냄. 따라서 $z_k$는 repair cell $k$에서 사용 가능한 서버 또는 유지보수 작업자의 수
• 요약하면 $M/M/z_k$는 엔티티 도착이 지수 분포를 따르고, 서비스 시간은 포아송 분포를 따름. 수리 셀 $k$에 여러 서버(이 경우 유지 보수 작업자)가 있는 큐잉 시스템을 의미합니다.

 

The analysis of resulting queuing systems provides the expected number of backorders $\mathbb{EBO}_n [·]$ for each SKU type $n (n = 1,..., N)$ which can be used to optimize $I_n$ (see Turan et al. (2020c) for details). However, to evaluate the expected number of backorders $\mathbb{EBO}_n [·]$ for larger repair cells (with the high number of workers $z_k$ and part types $N$) is not computationally feasible, thus we use the aggregation-based approximation proposed by Van Harten and Sleptchenko (2003).

• 결과 큐잉 시스템의 분석은 각 SKU 유형 $n(n = 1,..., N)$에 대해 예상 백오더 수 $\mathbb{EBO}_n [·]$를 제공하며, 이는 $I_n$을 최적화하는 데 사용할 수 있습니다(자세한 내용은 Turan et al. (2020c) 참조). 그러나 더 큰 수리 셀에 대한 예상 백오더 수 $\mathbb{EBO}_n [·]$를 평가하는 것은 계산 가능하지 않으므로 Van Harten과 Sleptencho(2003)가 제안한 집계 기반 근사치를 사용(aggregation-based approximation)합니다.
  근사치 계산법은 아래에서 언급

 

In each iteration of the greedy heuristic, the number of workers $z_k$ in repair cell $k$ increased by one to capture the trade-off between adding an additional worker to a cell and decreasing inventories of spares that are allocated to that cell. Iterations continue until employing an additional worker is not economical; i.e., the increased workforce doesn‘t lead to any spare inventory reduction.

• Greedy 휴리스틱의 각 iteration에서 수리 셀 $k$에 있는 작업자 수 $z_k$는 셀에 추가 작업자를 추가하는 것과 해당 셀에 할당된 예비 재고 감소 사이의 트레이드오프를 포착하기 위해 하나씩 증가($+1$)했습니다. 추가 작업자를 고용하는 것이 경제적이지 않을 때까지 반복됩니다. 즉, 인력 증가가 예비 재고 감소로 이어지지 않습니다.

 

4.6. Algorithm parameters and their values

The DRL parameters number of episodes($nEps$), and the number of time steps($τ$) in Table 4 are chosen by using a grid search over the values of 100, 200, 300, 500, 1000, 2500 for $n E ps$ and 32, 64, 128, 256, 512, and 1024 for $τ$ . The values that yield in reasonable running time and close to optimum solutions are reported. The $γ$ is chosen high not to discount the future rewards severely. Table 5 lists the used parameters for the deep Q-network. To control the stochastic behavior of the network and make training (which uses matrix calculations heavily), we used batch_size value of 32. The choice of the $η$ value is also critical to ensure the target network catches up with the policy network. The common approach is to choose a value between 0.1 and 0.00001 (Wu et al. 2019). We adopted the recommended setting by Kandel and Castelli (2020).

The number of input units $D$ for $D Q N$ depends on the number of SKUs $( N )$ used. Since the number of input units is at most 20 (see Sect. 6.1), only 2 hidden layers were enough to produce accurate results. The number of hidden units $h^{(l)}$ at $l^{th}$ layer depends on $D$ and is chosen using a grid search over possible values. The number of output units $C$ for the network is equal to the number of available actions. In Table 6, we provide the important parameter values used for the SA algorithm. To update the parameters of the networks, we used Adam optimizer. We refer the reader to Kingma and Ba (2017) for details of the Adam optimizer.

• 표 4의 DRL 매개변수 episode 수($nEps$)와 time steps 수( $τ$)는 $nEps$의 경우 100, 200, 300, 500, 1000, 2500, $τ$의 경우 32, 64, 128, 256, 512, 1024 값 이상의 그리드 검색을 사용하여 선택됩니다. 합리적인 실행 시간과 최적 솔루션에 가까운 값이 보고됩니다. $γ$는 미래 보상을 심각하게 할인하지 않기 위해 높게 선택됩니다. 표 5는 DQN에 사용되는 매개변수를 나열합니다. 네트워크의 확률적 동작을 제어하고 (행렬 계산을 많이 사용하는) 학습을 만들기 위해 32의 batch_size 값을 사용했습니다. $η$ 값의 선택은 Target Network가 Policy Network를 따라잡는 것을 보장하는 데도 중요합니다. 일반적인 접근 방식은 0.1에서 0.00001 사이의 값을 선택하는 것입니다(Wu et al. 2019). 저희는 Kandel and Castelli(2020)에서 권장하는 설정을 채택했습니다.
• $D Q N$에 대한 input size $D$는 사용된 SKU($N$)의 수에 따라 달라집니다. input unit의 수는 최대 20개이기 때문에(섹션 6.1 참조) 정확한 결과를 생성하기에 2개의 숨겨진 계층만 충분했습니다. $l^{th}$ 계층의 숨겨진 단위 $h^{(l)}$의 수는 $D$에 따라 달라지며 가능한 값에 대한 그리드 검색을 사용하여 선택됩니다. 네트워크의 output size $C$는 사용 가능한 action의 수($n(A)$)와 동일합니다. 표 6에서는 SA 알고리즘에 사용된 중요한 매개 변수 값을 제공합니다. 네트워크의 매개 변수를 업데이트하기 위해 Adam Optimizer를 사용했습니다. Adam Optimizer에 대한 자세한 내용은 Kingma and Ba(2017)를 참조하십시오.

 

5. Benchmark methods

We use two different sets of benchmark algorithms to compare the results of DRLSA. The first set of benchmarks includes three well-known meta-heuristic algorithms, namely a Simulated Annealing (SA), a Genetic Algorithm (GA), and a Variable Neighborhood Search (VNS). The SA algorithm by Kosanoglu et al. (2018) is used as the benchmark, which is an improved version of the basic SA algorithm that we use in this study. Further, the details of benchmark GA and VNS algorithms together with their parameter settings can be found in Turan et al. (2020b).

• 저희는 DRLSA의 결과를 비교하기 위해 두 가지 다른 벤치마크 알고리즘 세트를 사용합니다. 첫 번째 벤치마크 세트에는 세 가지 잘 알려진 메타 휴리스틱 알고리즘, 즉 SA, 유전 알고리즘 (GA) 및 가변 이웃 검색(VNS)이 포함됩니다. Kosanoglu et al. (2018)의 SA 알고리즘은 본 연구에서 사용하는 기본 SA 알고리즘의 개선된 버전인 벤치마크로 사용됩니다. 또한 벤치마크 GA 및 VNS 알고리즘과 매개변수 설정에 대한 자세한 내용은 Turan et al. (2020b)에서 확인할 수 있습니다.

 

In the second set of benchmarks, we consider a machine learning-based (ML-based) clustering algorithm with four variants (K-Median1, K-Median2, K-Median3, K-Median4). We use a K-Median Clustering as provided in Algorithm 3. Variant algorithms differentiate from each other in terms of clustering features they employ. We use different properties of parts (e.g., failure rates $λ_n$ , holding costs $h_n$ , and repair rates $μ_n$ ) as clustering features. Table 7 presents pseudo-codes for each variant are provided in Algorithms 4, 5, 6, and 7.

• 두 번째 벤치마크 세트에서는 4가지 변형(K-Median1, K-Median2, K-Median3, K-Median4)이 있는 기계 학습 기반(ML 기반) 클러스터링 알고리즘을 고려합니다. 저희는 Algorithm 3에 제공된 대로 K-Median 클러스터링을 사용합니다. 변형 알고리즘은 클러스터링 기능을 사용한다는 측면에서 서로 다릅니다. 저희는 클러스터링 기능으로 다양한 부품 속성(고장률 $λ_n$, 유지 비용 $h_n$, 복구율 $μ_n$)을 사용합니다. 표 7은 알고리즘 4, 5, 6, 7에 제공된 각 변형에 대한 유사 코드를 보여줍니다.
• K-Means 알고리즘은 중심이 더 이상 변하지 않을 때까지 중심이 가장 가까운 클러스터에 데이터 점을 반복적으로 할당합니다. 그런 다음 클러스터의 중앙값을 계산하고 그에 따라 중심을 업데이트합니다. 반복 후에도 중심이 변하지 않으면 알고리즘은 중단됩니다. 그 결과 각 클러스터가 중앙값과 연관되고 데이터 점과 각 중앙값 사이의 거리의 총합이 최소화됩니다.
• K-Median1: 세 집합의 값$(μ, λ,h)$을 취하여 정규화하고 특정 공식을 사용하여 요소 쌍 간의 거리를 계산한 다음 결과로 나온 거리 행렬에 K-중앙값 클러스터링 알고리즘을 적용합니다. 목표는 정규화된 공간에서의 거리를 기반으로 요소를 K 그룹으로 클러스터링 할 가능성이 높습니다.
• K-Median2: $μ$값의 집합을 취하여 원소 쌍들 사이의 제곱한 차이를 계산한 다음, K-중앙값 클러스터링 알고리즘을 결과 거리 행렬에 적용합니다. 목표는 원소들을 제곱한 차이를 바탕으로 K개의 그룹으로 클러스터링하는 것입니다 ($\mu$: 부품 고장 시 수리율)
• K-Median3: $\lambda$값의 집합을 취하여 원소 쌍들 사이의 제곱한 차이를 계산한 다음, K-중앙값 클러스터링 알고리즘을 결과 거리 행렬에 적용합니다. 목표는 원소들을 제곱한 차이를 바탕으로 K개의 그룹으로 클러스터링하는 것입니다 ($\lambda$: 부품 고장률)
• K-Median4: $h$값의 집합을 취하여 원소 쌍들 사이의 제곱한 차이를 계산한 다음, K-중앙값 클러스터링 알고리즘을 결과 거리 행렬에 적용합니다. 목표는 원소들을 제곱한 차이를 바탕으로 K개의 그룹으로 클러스터링하는 것입니다 ($h$: 단위 시간 당 부품의 여유 재고 인벤토리 보관 비용)

→ 세 가지 변수에 대한 중앙값 클러스터링을 통해 결과를 분석

 

6. Computational Study

To evaluate the performance of the proposed DRLSA approach, we conduct a detailed numerical analysis. Particularly, in Sect. 6.1, we define the experiment testbed employed in our analysis. Section 6.2 explores the solution quality of the approach by comparing it with total enumeration results. Then, Sect. 6.3 presents a detailed run time and convergence analysis. Next, in Sect. 6.4, we compare the total system cost achieved by the proposed DRLSA algorithm with the costs achieved by benchmark algorithms. Finally, in Sect. 6.5, we investigate capacity usage and cross-training policies.

• 제안된 DRLSA 접근 방식의 성능을 평가하기 위해 상세한 수치 분석을 수행합니다. 특히 6.1절에서는 분석에 사용된 실험 테스트베드 Testbed를 정의합니다. 6.2절에서는 총 열거 결과와 비교하여 접근 방식의 솔루션 품질을 탐색합니다. 그런 다음 6.3절에서는 자세한 실행 시간 및 수렴 분석을 제시합니다. 다음으로 6.4절에서는 제안된 DRLSA 알고리즘에 의해 달성된 총 시스템 비용을 벤치마크 알고리즘에 의해 달성된 비용과 비교합니다. 마지막으로 6.5절에서는 용량 사용 및 교차 훈련 정책을 조사합니다.

 

6.1. Testbed

Table 8  Testbed를 위한 문제 매개변수

We utilize the same testbed of instances as in Turan et al. (2020c) to investigate the effective- ness of the proposed DRLSA method. In this testbed, a full factorial design of experiment (DoE) with seven factors and two levels per factor is used as shown in Table 8. We test the proposed algorithm and all benchmarks with a total of 128 instances. In this testbed, initial workers $M$ denotes the minimum number of workers that have to be utilized in the maintenance facility. Further, we use two different patterns, namely completely random and independent (IND) and hyperbolically related (HPB) to generate the holding costs $h_n$. The HPB pattern reflects the cases in which expensive repairables are repaired less frequently. For the explicit definitions and derivation of test instances and factors, we refer the reader to the work of Turan et al. (2020c).

• 제안된 DRLSA 방법의 효율성을 조사하기 위해 Turan et al. (2020c)에서와 동일한 인스턴스 테스트 베드를 사용합니다. 이 테스트 베드에서는 Table 8과 같이 7개의 요인과 요인당 2개의 수준을 가진 실험의 완전 요인 설계(DoE)가 사용됩니다. 저희는 총 128개의 인스턴스로 제안된 알고리즘과 모든 벤치마크를 테스트합니다. 이 테스트 베드에서 초기 작업자 $M$는 유지 보수 시설에서 사용해야 하는 최소 작업자 수를 나타냅니다. 또한, 저희는 보유 비용 $h_n$를 생성하기 위해 두 가지 다른 패턴, 즉 완전 무작위 및 독립(IND)과 하이퍼볼릭 관련(HPB)을 사용합니다. HPB 패턴은 고가의 수리물이 수리되는 빈도가 낮은 경우를 반영합니다. 테스트 인스턴스 및 요인의 명시적인 정의와 유도는 Turan et al. (2020c)의 작업을 참조하십시오.

 

6.2. Optimality gaps and optimal solution behavior

In this section, we give an analysis for assessing the solution quality of the proposed DRLSA algorithm. We employ the testbed given in Sect. 6.1 to investigate the gap between DRLSA solutions and the optimal solutions. In order to create relatively small size test problems that can be solved by a brute force (total enumeration) approach, we randomly choose four, five, six, and seven SKUs from each case generated in the previous section. First, we investigate the gap between the minimum cost achieved by total enumeration (i.e. the optimal cost) and the DRLSA algorithm. The DRLSA algorithm achieves the optimal cost for all tested $512(4 × 128)$ cases.

• 이 섹션에서는 제안된 DRLSA 알고리즘의 솔루션 품질을 평가하기 위한 분석을 제공합니다. DRLSA 솔루션과 최적 솔루션 간의 격차를 조사하기 위해 섹션 6.1에 제공된 테스트 베드를 사용합니다. 브루트포스 접근 방식으로 해결할 수 있는 비교적 작은 크기의 테스트 문제를 만들기 위해 이전 섹션에서 생성된 각 사례에서 4, 5, 6, 7개의 SKU를 무작위로 선택합니다. 먼저 전체 iteration으로 달성한 최소 비용(최적 비용)과 DRLSA 알고리즘 간의 격차를 조사합니다. DRLSA 알고리즘은 테스트된 모든 $512(4 × 128)$ 사례에 대해 최적의 비용을 달성합니다.

 

We further investigate the optimal solution behavior. In particular, we inspect how the optimal number of repair cells (clusters) $K$ differs as the number of SKUs $N$ changes. We present the number of repair cells for each solved case in Fig. 6. We observe that the optimal number of repair cells never reaches the number of SKUs $N$ (such that dedicated design). Our results also indicate that the maintenance facility is divided into mostly two repair cells regardless of the number of SKUs $N$.

• 저희는 최적의 솔루션 동작을 추가로 조사합니다. 특히, 저희는 SKU $N$의 수가 변함에 따라 최적의 수리 셀 수(클러스터) $K$가 어떻게 다른지 검사합니다. 저희는 그림 6에서 각 solved case에 대한 수리 셀 수를 제시합니다. 저희는 최적의 수리 셀 수가 SKU $N$의 수($N=K$ 즉, 전용 설계)에 절대 도달하지 않는다는 것을 관찰했습니다. 저희의 결과는 또한 유지 보수 시설이 SKU $N$의 수에 관계없이 대부분 두 개의 수리 셀로 분할됨을 나타냅니다. ($K=2$)

 

6.3. Runtime and convergence analysis

In this subsection, we comment on the convergence and runtime of DRLSA, and SA and RL stages. We implemented all algorithms discussed in this paper in Python programming language and ran them on a desktop computer with 4 core 3.60 GHz CPU and 8 GB RAM.

• 이 하위 절에서는 DRLSA, SA 및 RL 단계의 융합 및 런타임에 대해 설명합니다. 본 논문에서 논의된 모든 알고리즘을 파이썬 프로그래밍 언어로 구현하여 4코어 3.60GHz CPU와 8GB RAM을 갖춘 데스크톱 컴퓨터에서 실행했습니다.

 

Table 9 shows the effect of the problem factors on runtime. Under all problem factors, we observe that most of the runtime (nearly 85%) is occupied by SA rather than RL stages. It should be also noted that on average runtime of DRLSA increases nearly twice when Cross-training cost ($βn$) is reduced to 0.01 from 0.10. Further, another noticeable runtime fluctuation occurs when the minimum holding cost ($h{\text{min}}$) is increased from 1 to 100.

• 표 9는 런타임에 대한 문제 요인의 영향을 보여줍니다. 모든 문제 요인에서 대부분의 런타임(거의 85%)은 RL 단계가 아닌 SA가 차지하는 것으로 관찰됩니다. DRLSA의 평균 런타임은 교차 훈련 비용($βn$)이 0.10에서 0.01로 감소할 때 거의 두 배 증가한다는 점도 유의해야 합니다. 또한 최소 유지 비용($h{\text{min}}$)이 1에서 100으로 증가할 때 또 다른 눈에 띄는 런타임 변동이 발생합니다.

 

For illustrative purposes, the total cost $TC$ convergence is shown for a single case in Fig. 7. In this particular case, DRLSA starts with a sharp decrease in total cost at early episodes (until around episode 10) and continues to converge to the best solution until around Episode 260. Figure 7 also presents how cost convergence occurs in a single episode between RL and SA stages. For the case we presented, it is clear that the SA stage does not perform well after iteration 600, which may indicate that initial temperature $T_o$ might be reduced without affecting solution quality.

• 설명을 위해 Fig. 7은 단일 사례에 대한 총 비용 $TC$ 수렴을 보여줍니다. 이 경우 DRLSA는 초기 에피소드(10회 경까지)에서 총 비용이 급격히 감소하는 것으로 시작하여 260회 경까지 최상의 솔루션으로 계속 수렴합니다. Fig. 7은 또한 RL과 SA 단계 사이에서 단일 에피소드에서 비용 수렴이 어떻게 일어나는지 보여줍니다. 저희가 제시한 경우 600번 반복 후 SA 단계가 잘 수행되지 않는 것이 분명하며, 이는 솔루션 품질에 영향을 주지 않고 초기 온도 $T_o$가 감소할 수 있음을 나타낼 수 있습니다.

 

6.4. Performance comparisons

In this section, the performance of the proposed algorithm is evaluated by comparing it with a set of benchmark algorithms described in Sect. 5. We present a detailed analysis of cost reductions achieved by the proposed DRLSA algorithm and factors affecting the performance.

• 이 절에서는 제안된 알고리즘의 성능을 섹션 5에서 설명한 벤치마크 알고리즘 세트와 비교하여 평가합니다. 제안된 DRLSA 알고리즘에 의해 달성된 비용 절감과 성능에 영향을 미치는 요인에 대한 자세한 분석을 제시합니다.

 

We first assess how DRLSA performs in cost compared to benchmark algorithms. Fig- ure 8 presents pair-wise performance comparisons of DRLSA to benchmark algorithms. In particular, we present the number of cases DRLSA outperforms, underperforms, and performs the same as benchmark algorithms in achieving minimum cost. In most of the cases, the DRLSA algorithm is superior to benchmark algorithms. The second best performing algorithm is SA which outperforms the DRLSA in 35 out of 128 cases, while the DRLSA is superior in 54 out of 128 cases. Table 10 presents the number of cases lowest cost achieved by each algorithm under each of the problem factors. For each case, multiple algorithms may achieve the minimum cost.

• 저희는 먼저 DRLSA가 벤치마크 알고리즘과 비교하여 비용 면에서 어떻게 성능을 발휘하는지 평가합니다. 그림 8은 벤치마크 알고리즘에 DRLSA의 쌍별 성능 비교를 제시합니다. 특히 DRLSA가 최소 비용을 달성하는 데 있어 벤치마크 알고리즘보다 성능, 성능 및 성능이 우수한 경우의 수를 제시합니다. 대부분의 경우 DRLSA 알고리즘이 벤치마크 알고리즘보다 성능이 우수합니다. 두 번째로 성능이 뛰어난 알고리즘은 SA로 128개 사례 중 35개 사례에서 DRLSA를 능가하는 반면, DRLSA는 128개 사례 중 54개 사례에서 우수합니다. 표 10은 각 문제 요인에서 각 알고리즘이 달성한 가장 낮은 비용을 달성한 경우의 수를 제시합니다. 각 사례에 대해 여러 알고리즘이 최소 비용을 달성할 수 있습니다.

 

The DRLSA is the best performing algorithm in achieving the minimum cost 55 out of 128 cases, followed by SA with 39 out of 128 cases. GA algorithm achieves the lowest total cost in 29 of 128 cases, VNS algorithm achieves the lowest total cost in 20 of 128 cases, and K-Median1, K-Median2, K-Median3, K-Median4 algorithms achieve the lowest total cost in 15, 11, 16, 13 of 128 cases respectively. We also observe that fully flexible design achieves the lowest total cost in 11 of 128 cases, and dedicated designs never achieve the minimum cost. We also observe that GA and VNS algorithms are extremely sensitive to the number of SKUs N while SA and DRLSA are relatively less sensitive. Another notable result is the increase in workforce cost/base-level salary (α) increases the performance of DRLSA and VNS, decreases GA, and doesn’t affect SA. In general, SA is the least sensitive algorithm to the problem factors.

• DRLSA는 128건 중 최소 비용 55건을 달성하는 데 가장 뛰어난 성능을 보이는 알고리즘이며, SA는 128건 중 39건으로 그 뒤를 이룹니다. GA 알고리즘은 128건 중 29건에서 총 비용이 가장 낮고, VNS 알고리즘은 128건 중 20건에서 총 비용이 가장 낮으며, K-Median1, K-Median2, K-Median3, K-Median4 알고리즘은 128건 중 15건, 11건, 16건, 13건에서 각각 총 비용이 가장 낮습니다. 또한 완전 유연한 설계는 128건 중 11건에서 총 비용이 가장 낮으며, 전용 설계는 최소 비용을 달성하지 못한다는 것을 관찰했습니다. 또한 GA 및 VNS 알고리즘은 SKU N의 수에 매우 민감한 반면 SA 및 DRLSA는 상대적으로 덜 민감하다는 것을 관찰했습니다. 또 다른 주목할 만한 결과는 인력 비용/기본 수준 급여($α$)의 증가로 DRLSA 및 VNS의 성능이 증가하고 GA가 감소하며 SA에 영향을 미치지 않는다는 것입니다. 일반적으로 SA는 문제 요인에 가장 덜 민감한 알고리즘입니다.

 

 

We next investigate how the total cost achieved by DRLSA compares to the benchmark algorithms. Figure 9 presents the total cost of DRLSA minus the total cost of the benchmark algorithm. The minimum costs achieved by SA and VNS are relatively close to DRLSA.

• 다음으로 DRLSA에 의해 달성된 총 비용이 벤치마크 알고리즘과 어떻게 비교되는지 알아봅니다. 그림 9는 DRLSA의 총 비용에서 벤치마크 알고리즘의 총 비용을 뺀 값을 제시합니다. SA와 VNS에 의해 달성된 최소 비용은 DRLSA에 비교적 근접합니다.

 

In Figs. 10a and b, we present cost reductions achieved by each algorithm in comparison to dedicated and fully flexible designs, respectively. The cost reduction amounts are sensitive to problem factors in comparison to both dedicated and fully flexible design. In particular, all algorithms attain the highest cost reduction compared to the dedicated design when $N$ is large (20), $M$ is small (5), workforce cost is large ($100h_{\text{max}}$), and cross-training cost is small ($0.01α$).

• 그림 10a와 b에서는 각각 전용 설계($N=K$)와 완전 유연 설계($K=1$)에 비해 각 알고리즘이 달성한 비용 절감량을 제시합니다. 비용 절감량은 전용 설계와 완전 유연 설계 모두에 비해 문제 요인에 민감합니다. 특히 모든 알고리즘은 $N$이 크고(20), $M$이 작으며(5), 인력 비용이 크고($100h_{\text{max}}$), 교차 훈련 비용이 작을 때($0.01α$) 전용 설계에 비해 가장 높은 비용 절감을 달성합니다.

 

Presumably, when $N$ is large, dedicated design results in lower utilization of workers. Similarly, when workforce cost is higher, the cost of dedicated design results in a larger cost due to the extensive number of workers. When $M$ is small, the additional workforce demand increases the cost due to the requirements of the dedicated design.

Finally, when cross-training cost is small instead of having many maintenance workers dedicated to a single SKU type, cross-training workforce are more cost-effective. On the other hand, the cost reduction is more sensitive to cross-training costs in comparison to fully flexible design due to an increase in training cost (compensation payment) of workers for each SKU. We can also remark that cost reduction of SA, VNS, GA, and DRLSA are substantially larger than ML-based algorithms.

• 아마도 $N$가 클 때 전용 설계($N=K$)는 작업자의 활용도를 낮추는 결과를 낳습니다. 마찬가지로 작업자 비용이 높을 때 전용 설계 비용은 광범위한 작업자 수로 인해 더 큰 비용을 초래합니다. $M$이 작을 때 추가 작업자 수요는 전용 설계의 요구 사항으로 인해 비용을 증가시킵니다. 마지막으로 단일 SKU 유형에 많은 유지 보수 작업자를 두는 대신 교차 훈련 비용이 작을 때 교차 훈련 작업자가 비용 효율적입니다. 반면 비용 절감은 SKU별 작업자의 훈련 비용(보상 지불) 증가로 인해 완전 유연 설계에 비해 교차 훈련 비용에 더 민감합니다. 또한 SA, VNS, GA 및 DRLSA의 비용 절감이 ML 기반 알고리즘보다 상당히 크다는 점을 언급할 수 있습니다.

 

We also evaluate the performance of DRLSA for larger problem instances with 50 and 100 SKUs. We compare the achieved objective function values of DRLSA and ML-based algorithms. We observe that DRLSA achieves the best cost reduction in comparison to fully flexible design followed by K-median3, K-median2, K-median1, and K-median4 in 50 SKUs case. Nevertheless, in 100 SKUs case, K-median3 achieves the best cost reduction followed by DRLSA, K-median2, K-median1, and K-median4. The detailed results are presented in Table 11. The performance of the DRLSA algorithm may be improved for larger SKU numbers (larger search space) by increasing the iteration and episode numbers.

Furthermore, the proposed DRLSA algorithm provides the solutions for the larger maintenance planning problems in an acceptable time.

• 또한 50개와 100개의 SKU가 있는 더 큰 문제 인스턴스에 대한 DRLSA의 성능을 평가합니다. 저희는 DRLSA와 ML 기반 알고리즘의 달성된 목적 함수 값을 비교합니다. 저희는 DRLSA가 50개의 SKU 사례에서 K-median3, K-median2, K-median1 및 K-median4에 이어 완전 유연한 설계($K=1$)에 비해 최고의 비용 절감을 달성하는 것을 관찰했습니다. 그럼에도 불구하고 100개의 SKU 사례에서 K-median3은 DRLSA, K-median2, K-median1 및 K-median4에 이어 최고의 비용 절감을 달성합니다. 자세한 결과는 표 11에 나와 있습니다. 반복 및 에피소드 번호를 증가시켜 더 큰 SKU 번호(더 큰 검색 공간)에 대해 DRLSA 알고리즘의 성능을 향상시킬 수 있습니다.
• 또한 제안된 DRLSA 알고리즘은 허용 가능한 시간 내에 더 큰 유지보수 계획 문제에 대한 해결책을 제공합니다.

 

6.5. Capacity usage and cross-training analysis

This section investigates how repair cell formation and cross-training depend on problem parameters and solution algorithms. In Table 12, we present the average number of workers utilized per case, the average number of repair cells in the optimized solution, and the average number of skills per worker. Interestingly, the number of repair cells formed with ML-based algorithms is extremely sensitive to cross-training cost factor levels, yet SA, VNS, GA, and DRLSA are relatively less sensitive to cross-training cost factor levels. Specifically, when the cross-training cost increased from $0.01α$ to $0.1α$, the average number of repair cells is nearly doubled.

• 이 절에서는 수리 셀 형성과 교차 훈련이 문제 매개변수와 솔루션 알고리즘에 어떻게 의존하는지 조사합니다. 표 12에서는 사례당 평균 활용된 작업자 수, 최적화된 솔루션의 평균 수리 셀 수, 작업자당 평균 기술 수를 제시합니다. 흥미롭게도 ML 기반 알고리즘으로 형성된 수리 셀의 수는 교차 훈련 비용 요소 수준에 매우 민감하지만 SA, VNS, GA 및 DRLSA는 교차 훈련 비용 요소 수준에 상대적으로 덜 민감합니다. 특히 교차 훈련 비용이 $0.01α$에서 $0.1α$로 증가하면 평균 수리 셀 수는 거의 두 배로 증가합니다.

 

We also observe that the numbers of repair cells formed with SA, VNS, GA, and DRLSA are more sensitive to the number of SKUs $N$ (on average 75% increase in the average number of repair cells formed when the number of SKUs is increased from 10 to 20). Surprisingly, the numbers of repair cells formed with K-Median1 and K-Median4 decrease as the number of SKUs increases, while a slight increase is observed for K-Median2 and K-Median3.

• 또한 SA, VNS, GA 및 DRLSA로 형성된 수리 셀의 수가 SKU $N$(SKU 수를 10개에서 20개로 늘릴 때 형성되는 평균 복구 셀 수의 평균 75% 증가)에 더 민감하다는 것을 관찰했습니다. 놀랍게도 SKU가 증가함에 따라 K-Median1 및 K-Median4로 형성된 복구 셀의 수는 감소하는 반면 K-Median2 및 K-Median3의 경우 약간 증가하는 것으로 관찰되었습니다.

 

Average Cross-Training Percentages 평균 교차 훈련 백분율

Another question we explore is how much cross-training would be enough under various problem factors. Figure 11 shows the average cross-training percentages achieved by each algorithm for each problem factor. Our results demonstrate that the average cross-training percentages of ML-based algorithms are larger compared to other algorithms. Although the differences are not large, the cross-training percentage order of other algorithms is DRLSA, SA, VNS, and GA from the largest to the smallest, respectively, for almost all problem factors. The average cross-training percentage is highly sensitive to cross-training costs $β_n$ for all algorithms. More specifically, the average cross-training percentages of ML-based algorithms are tripled as cross-training costs increased from $0.01α$ to $0.1α$, whereas cross- training percentages of other algorithms are nearly doubled.

The number of SKUs $N$ is another essential problem factor that affects the average cross-training percentage. In particular, when the number of SKUs is increased from 10 to 20, the average cross-training percentage is diminished by half for DRLSA and other meta-heuristics. However, an increase is observed for K-Median1, K-Median2, and K-Median4, and a decrease for K-Median3 as the number of SKUs increases 10 to 20. This result arguably arises due to the clustering features of algorithms. K-Median3 uses the failure rate of the in-use part as a clustering feature ($λ_n$), while other algorithms use the repair rate of the failed part ($μ_n$ ), the inventory holding cost ($h_n$ ), or both.

• 저희가 탐구하는 또 다른 질문은 다양한 문제 요인 하에서 얼마나 많은 교차 훈련이 충분한지입니다. 그림 11은 각 문제 요인에 대해 각 알고리즘이 달성한 평균 교차 훈련 백분율을 보여줍니다. 저희의 결과는 ML 기반 알고리즘의 평균 교차 훈련 백분율이 다른 알고리듬에 비해 더 크다는 것을 보여줍니다. 차이는 크지 않지만 거의 모든 문제 요인에 대해 다른 알고리즘의 교차 훈련 백분율 순서는 각각 가장 큰 것에서 가장 작은 것으로 DRLSA, SA, VNS 및 GA입니다. 평균 교차 훈련 백분율은 모든 알고리즘의 교차 훈련 비용 $β_n$에 매우 민감합니다. 보다 구체적으로, ML 기반 알고리즘의 평균 교차 훈련 백분율은 $0.01α$에서 $0.1α$로 증가함에 따라 3배 증가하는 반면, 다른 알고리즘의 교차 훈련 백분율은 거의 2배 증가합니다.
• SKU $N$의 수는 평균 교차 훈련 백분율에 영향을 미치는 또 다른 필수 문제 요소입니다. 특히 SKU의 수가 10개에서 20개로 증가하면 DRLSA 및 기타 메타 휴리스틱의 경우 평균 교차 훈련 백분율이 절반으로 감소합니다. 그러나 K-Median1, K-Median2 및 K-Median4의 경우 증가하고 SKU의 수가 10개에서 20개로 증가함에 따라 K-Median3의 경우 감소하는 것으로 관찰됩니다. 이 결과는 거의 틀림없이 알고리즘의 클러스터링 기능으로 인해 발생합니다. K-Median3는 사용 중인 부분의 실패율( $λ_n$)을 클러스터링 기능으로 사용하는 반면, 다른 알고리듬은 실패 부분의 복구율($μ_n$), 재고 유지 비용($h_n$) 또는 둘 모두를 사용합니다.

 

7. Conclusions and Future Research

The design of effective maintenance planning is crucial to ensure high asset availability with the minimum cost. In this paper, we develop a heuristic algorithm inspired by DRL to solve a joint maintenance planning problem by taking into account several decisions simultaneously, including workforce planning, workforce training, and spare parts inventory management. This work is an initial attempt to improve solution algorithms using DRL for corrective maintenance problems.

• 최소의 비용으로 높은 자산 가용성을 보장하기 위해서는 효과적인 유지 보수 계획 설계가 중요합니다. 본 논문에서는 인력 계획, 인력 교육 및 예비 부품 재고 관리 등 여러 의사 결정을 동시에 고려하여 공동 유지 보수 계획 문제를 해결하기 위해 DRL에서 영감을 얻은 휴리스틱 알고리즘을 개발합니다. 이 작업은 DRL을 사용하여 수정 유지 보수 문제에 대한 솔루션 알고리즘을 개선하기 위한 초기 시도입니다.

 

The computational results show that the proposed solution algorithm is promising in solving the defined problem. Particularly, the proposed DRLSA algorithm obtains a better objective function value (total cost) than well-known meta-heuristic algorithms (SA, GA, VNS) and machine learning-based clustering algorithms (K-Median1, K-Median2, K-Median3, and K-Median4). Our work reveals that there exists a great potential in the application of machine learning to optimization. In particular, machine learning-enforced optimization algorithms may provide relatively better solutions. We note that the performance of algorithms is sensitive to problem parameters. Moreover, parameters that affect the performance of algorithms may differ for each algorithm. For example, the increase in work- force cost/base-level salary ($α$) increases the performance of DRLSA and VNS, decreases GA, but does not affect SA.

• 계산 결과는 제안된 솔루션 알고리즘이 정의된 문제를 해결하는 데 유망하다는 것을 보여줍니다. 특히, 제안된 DRLSA 알고리듬은 잘 알려진 메타 휴리스틱 알고리듬(SA, GA, VNS) 및 기계 학습 기반 클러스터링 알고리듬(K-Median1, K-Median2, K-Median3, K-Median4)보다 더 나은 객관적 함수 값(총 비용)을 얻습니다. 저희의 연구는 기계 학습을 최적화에 적용하는 데 큰 잠재력이 있음을 보여줍니다. 특히, 기계 학습이 강제하는 최적화 알고리듬은 상대적으로 더 나은 솔루션을 제공할 수 있습니다. 저희는 알고리듬의 성능이 문제 매개변수에 민감하다는 점에 주목합니다. 또한 알고리듬의 성능에 영향을 미치는 매개변수는 알고리듬마다 다를 수 있습니다. 예를 들어, 작업력 비용/기본 수준 급여($α$)의 증가는 DRLSA와 VNS의 성능을 증가시키고 GA를 감소시키지만 SA에는 영향을 미치지 않습니다.

 

The studied joint maintenance planning problem has a few major limitations. First, it is assumed that the failure rates of parts are constant throughout their lifetime. However, a more realistic modeling would consider the aging of parts in-use and adjust the failure rates as a function of time. Second, the model is analyzed under static policies (e.g. routing of failed parts in the maintenance facility) to ensure the computational tractability of the queuing approximations.

• 연구된 공동 유지 보수 계획 문제에는 몇 가지 주요 한계가 있습니다. 첫째, 부품의 고장률은 수명 전반에 걸쳐 일정하다고 가정합니다. 그러나 보다 현실적인 모델링은 사용 중인 부품의 노후화를 고려하고 고장률을 시간의 함수로 조정합니다. 둘째, 모델은 정적 정책(예: 유지 보수 시설의 고장 부품 라우팅) 하에서 분석되어 큐잉 근사치의 계산 추적성을 보장합니다.

 

All of the above-listed computational challenges arising due to the analysis of queuing models could be alleviated by modeling repairable supply chains (including the repair shop) via a simulation model and coupling this simulation model with DRL. This is a niche area in the current literature that enables decision-maker to analyze and optimize dynamic problems under uncertainty. Further, another possible extension could be improving the DRLSA algorithm by exploiting the great potentials of the other reinforcement learning methods such as SARSA (State-Action-Reward-State-Action) to increase solution quality while reducing the runtime.

• 큐잉 모델 분석으로 인해 발생하는 위에 나열된 모든 계산 문제는 시뮬레이션 모델을 통해 복구 가능한 공급망(수리점 포함)을 모델링하고 이 시뮬레이션 모델을 DRL과 결합하여 완화할 수 있습니다. 이는 불확실성 하에서 의사 결정자가 동적 문제를 분석하고 최적화할 수 있도록 하는 현재 문헌의 틈새 영역입니다. 또한 SARSA(State-Action-Reward-State-Action)와 같은 다른 강화 학습 방법의 큰 잠재력을 활용하여 DRLSA 알고리즘을 개선하는 동시에 런타임을 줄이면서 솔루션 품질을 높이는 또 다른 확장이 될 수 있습니다.

 

Additionally, it might be worthwhile to integrate the DRL algorithm with other meta-heuristics such as GA and VNS.

• 또한 DRL 알고리즘을 GA 및 VNS와 같은 다른 메타 휴리스틱과 통합하는 것도 가치가 있을 수 있습니다.