안녕하세요. 교내대회인 반응속도탐구대회에 자연과학계열의 친구와 함께 참가했습니다. 주제는 아황산수소나트륨(NaHSO3)과 아이오딘산칼륨(KIO3)의 반응속도에 대한 탐구였습니다. 흔히 아이오딘(이전 요오드) 시계반응이라고도 합니다. 제가 화학에도 관심이 있었기 때문에 교내대회 후 확장연구를 진행하고 싶어서 흔쾌히 하자고 했습니다.

대회 기간 중에는 교내 화학실험실에서 실험을 할 수 있도록 지원해주었습니다.

먼저 실험에 대해 전반적인 내용부터 말씀드리도록 하겠습니다. (보고서 내용입니다)
I. 실험지식(이론)

반응 속도란, 반응이 빠르게 또는 느리게 일어나는 정도를 의미하며, 일정한 시간 동안 변화된 반응물이나 생성물의 농도를 측정하여 나 타낸다. 그리고 반응 속도는 크게 평균 반응 속도와 순간 반응 속도로 나눠진다. 위 식에서 k는 속도 상수, m과 n은 반응 차수이다. 반응 차수는 실험에 의해 결정된다. 평균 반응 속도란, 반응이 진행된 구간의 농도 변화를 반응이 진행된 시간으로 나누어 나타 낸 속도이며, 순간 반응 속도란, 특정 시간에서의 반응 속도이다. 반응 속도는 ‘반응 물의 농도 변화/반응시간' 혹은 ‘생성물의 농도 변화/반응시간'으로 구할 수 있다.
반응 속도에 영향을 주는 요소는 크게 세 가지로 나눌 수 있다. 고체, 액체, 기체에 공 통적으로 영향을 주는 요소는 온도이다. 부가적으로 고체의 경우 두 물질의 표면적에 따라 반응하는 속도가 달라질 수 있고, 액체의 경우 두 용액의 밀도(농도)에 따라 반응 하는 속도가 달라질 수 있고, 기체의 경우 가해지는 압력이 반응하는 속도에 영향을 미칠 수 있다.
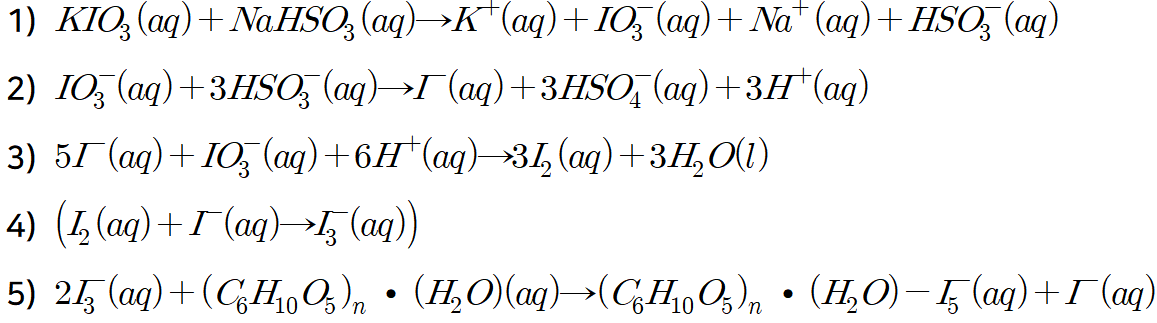
아황산수소나트륨과 아이오딘산칼륨의 화학반응식입니다. 다단계반응으로 5단계에 걸쳐 일어납니다.
식 1)은 물에서 이온이 녹는 용해과정입니다.

식 2)에서는 IO3-가 환원, HSO3-가 산화되고, 식 3)에서 I-가 환원, IO3-가 산화되는 산화환원반응입니다.
식 4)는 매우 빠른 반응이며, 아이오딘 분자와 아이오딘화 이온이 만나 삼아이오딘화 이온이 되는 반응입니다.

식 5)는 우리가 눈으로 볼 수 있는 유일한 반응입니다. 삼아이오딘화이온과 녹말이 물리적 결합을 하게 되어 파란 파장의 빛 스펙트럼을 반사하여 파랗게 보이게 됩니다.

II. 가설설정
가설 1. 반응물의 온도가 높을수록 반응 속도가 빨라질 것이다.
조작변인 : 반응물인 아황산수소나트륨과 아이오딘산칼륨 수용액의 온도
통제변인 : 반응물의 양, 주변온도, 압력
조작변인인 온도만 조절함으로서 온도변화에 따른 반응속도의 변화를 관찰한다.
가설 2. 아이오딘산칼륨 수용액의 농도가 높을수록 반응 속도가 빠를 것이다.
조작변인 : 아이오딘산칼륨 수용액의 농도(아이오딘산칼륨, 증류수 용량)
통제변인 : 아황산수소나트륨의 용량, 반응물의 온도, 주변온도, 반응물의 양, 압력
조작변인인 농도만 조절함으로서 농도변화에 따른 반응속도의 변화를 관찰한다.
III. 시약 및 기구
[시약]
▸아황산수소나트륨 (NaHSO3 , 분자량 104.06, CAS no : 7631-90-5)
위험성 : H318, P280, P305+P351+P338, P310
사용량 : 0.05M 수용액을 실험에 사용하기 위해 1L 당 총 5.2g(=104.06×0.05)을 사용한다.
▸아이오딘산칼륨 (KIO3 , 분자량 214, CAS no : 7758-05-6)
위험성 : H3O2, P264, P270, P301+P312, P330, P501
사용량 : 0.05M 수용액을 실험에 사용하기 위해 1L 당 총 10.7g(214×0.05) 사용
▸녹말 ((C6H10O5)n , 분자량 약 5만 ~ 20만, CAS no : 9005-25-8)
위험성 : 없음
사용량 : 아황산수소나트륨-아이오딘산칼륨 반응실험(농도 및 온도 조작) 용액 제조 시 90mL 사용 즉, 녹말 1% 수용액 100mL 제조를 위해서 증류수 100mL와 녹말 1g이 필요
▸증류수(H2O), 분자량 18, CAS no : 7732-18-5)
위험성 : 없음
사용량 : 아황산수소나트륨-녹말 용액제조 용액 당 1L 사용 = 1L 아이오딘산칼륨 용액제조 용액 당 1L 사용 = 1L 녹말 1% 용액 제조 용액 당 100mL 사용 = 100mL 실험1 회 당 각각 8, 16, 24, 32mL = 80mL 실험2 회 당 16mL 사용 = 80mL (총 5회)
∴ 총 2,260mL 사용
[기구]

IV. 실험 설계
[용액 제조]
실험 시작 전, 실험에 사용할 용액을 제조한다.

1. 녹말 1% 용액
1) 증류수 100g이 담긴 500mL 비커에 녹말 1g을 넣는다.
2) 마그네틱바를 넣고 교반기를 이용해 녹말을 녹여준다.
2. 용액 A(0.05M 아황산수소나트륨 수용액 + 녹말)
1) 증류수 600mL가 담긴 1000mL 삼각플라스크에 5.2g의 아황산수소나트륨을 넣는다.
2) 녹말 1% 용액 90mL를 삼각플라스크에 넣는다.
3) 증류수를 더 부어 1000mL를 맞추어준 후 유리막대로 저어 녹여준다.
3. 용액 B(0.05M 아이오딘산칼륨 수용액)
1) 증류수 600mL가 담긴 1000mL 삼각플라스크에 10.7g의 아이오딘산칼륨을 넣는다.
2) 증류수를 더 부어 1000mL를 맞추어준 후 유리막대로 저어 녹여준다.
단, 모든 용액 제조 시 상온에서의 기준이 되는 용액의 온도가 달라질 수 있으므로 가열하지 않는다.
[실험 1] 가설 1을 증명하기 위해 시행한다.
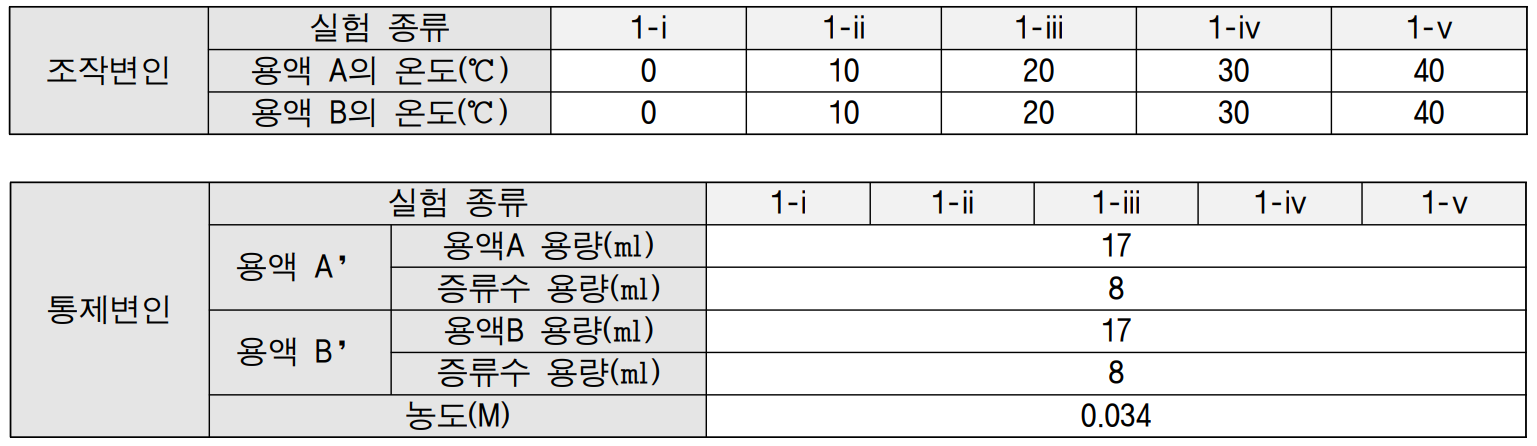
1. 비커 50mL에 위 표와 같은 농도의 용액 A‘와 용액 B’를 각각 5개씩 옮겨 담는다. (용액 A’와 용액 B’는 각각 용액 A와 용액 B에 증류수를 위 표와 같이 섞는다. 또한 각 비커에 번호를 표기한다.)

2. 0℃, 10℃, 20℃의 비커는 얼음 중탕을 이용해 온도를 낮추어준다. 이때, 온도계를 이용해 정확한 온도를 맞춘다.
3. 30℃, 40℃의 비커는 교반기를 이용해 온도를 높여준다. 이때, 온도계를 이용해 정확한 온도를 맞추고 온도가 맞추어지면 용액 A를 용액 B의 비커에 붓는다.
4. 용액이 부어져 들어가는 순간부터 용액의 색이 바뀌기 시작하는 순간까지의 시간을 측정한다. (정밀한 측정을 위해 영상을 촬영한 후 3번 측정한다.)
[실험 2] 가설 2를 증명하기 위해 시행한다.

1. 비커 50mL에 위 표와 같은 농도를 맞추기 위해 일정량의 용액 A와 용액 B를 각각 비커에 옮겨 담는다. (각 비커에 번호를 표기한다.) 이후 증류수를 부어 용액 A’와 용액 B’를 제조한다. (총 용량을 맞추어준다.)
2. 같은 농도끼리 용액 A를 용액 B의 비커에 붓는다.
3. 용액이 부어져 들어가는 순간부터 용액의 색이 바뀌기 시작하는 순간까지의 시간을 측정한다. (정밀한 측정을 위해 영상을 촬영한 후 3번 측정한다.)
V. 실험 결과
[실험 사진]

[실험 과정 중 관찰 내용]
실험의 결과는 온도가 증가할수록, 농도가 증가할수록 반응속도가 빨라졌다. 가설 1과 가설 2를 실험 1과 실험 2로 증명하였다.
[실험 1 결과]

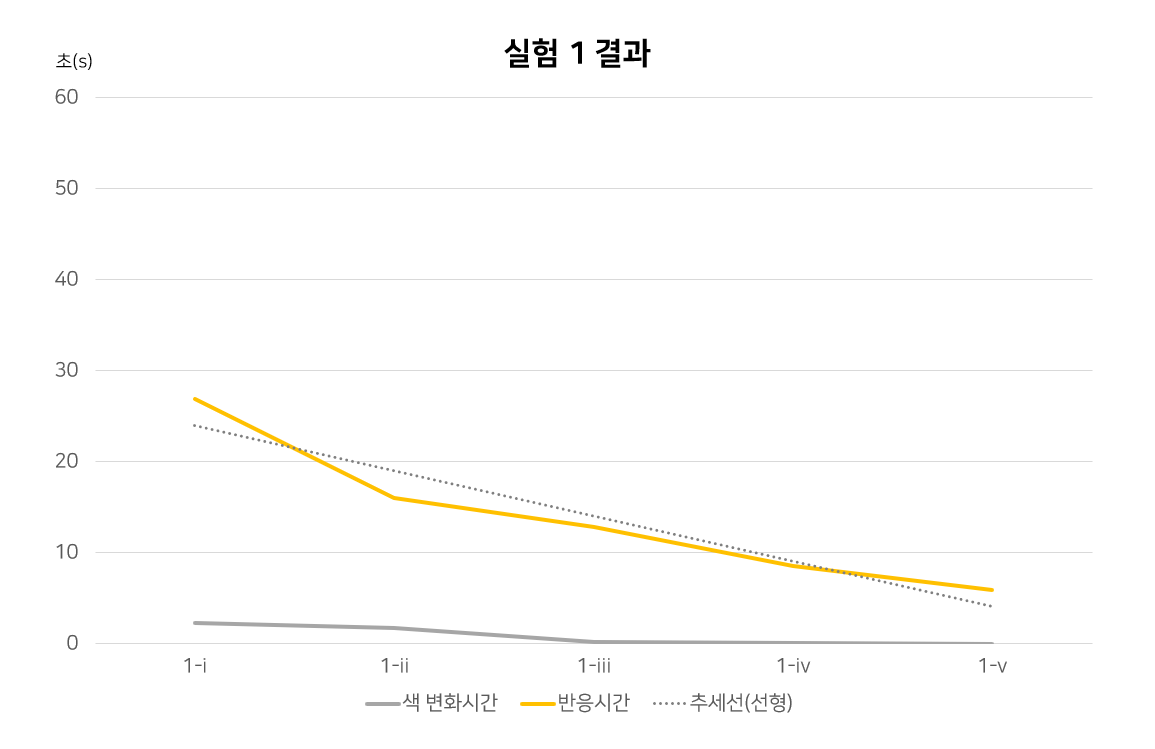
[실험 2 결과]


실험 결과에 대한 영상입니다. 한눈에 비교할 수 있도록 편집해보았습니다.
VI. 실험 결과에 대한 논의 및 결론
[실험 과정 중 관찰 내용 분석]
실험 1에서 온도가 증가하면 이에 비례하여 반응속도도 증가한다. 선형 추세선을 도입 하여 보면 온도와 반응속도는 거의 선형으로 증가한다. 실험 2에서 농도가 증가하면 반응속도도 증가한다. 거듭제곱형 추세선을 도입하여 보면 추세선이 선형으로 나타나 므로 반응차수가 2차이며, 농도와 반응속도는 제곱의 반비례 관계임을 알 수 있다.
[오차 원인]
1. 용액 제조 시 용질 불완전용해로 인한 농도의 미세한 차이
2. 실험 1(온도 조작)에서 용액 온도의 미세한 차이 및 이동과정에서의 온도 변화
3. 각각의 메니스커스 차이로 인한 오차 및 비커에 남은 용액으로 인한 농도 변화
[반응 속도의 차수 유추하기]
실험 I-iv와 I-i에서 농도가 0.026M에서 0.05M으로 약 2배가 될 때 용액 A, B 혼합용액 의 반응속도는 23.34s에서 6.21s로 약 ¼배가 된다. 즉 반응차수는 2차이다. (반응차수를 계산해주면 log(623/2309)÷ log(13/25)=2.0033) 혼합용액의 반응차수가 2이므로 m+n=2 이다. 용액 A와 B의 농도가 같으므로 m=n이다. m+n=2이므로 m=n=1.00이다. 즉 반응속도식은 v=k[IO3-]^m[HSO3-]^n이다. 실험 I-i에서 혼합용액의 몰농도(M)을 구하면 0.05×(0.025+0.025)/0.05이므로 M=5×10^-3 반응속도인 6.23과 농도가 4배 변했으므로 4로 나누어주면 v=2.006×10^-4M/s이다. 속도상수 k를 구해주면 2.006×10^-4=k[IO3-]^m[HSO3-]^n=k×0.05×0.05=0.0025k 즉, 속도상수 k=0.802이다. 또한 속도상수는 온도에 정비례하여 변한다.
VII. 참고문헌
∘ ywpop.tistory.com/2675 [반응 속도식 해석]
∘ msds.kosha.or.kr/kcic/msdssearchMsds.do [시약정보 확인]
∘ L.R. Summerlin, and J.L. Ealy, Jr. (1988) Chemical Demonstrations(American Chemical Society) Vol. 1: 103 [화학반응식 참고]
∘ m.blog.naver.com/PostView.nhn?blogId=green1&logNo=50189726118&proxyReferer=https%3 A%2F%2Fwww.googe.com%2F [시계반응 반응속도 계산 참고]
여기까지가 실험보고서입니다.
저는 여기서 더 나가 반응속도와 관련된 프로그램을 파이썬 (Python)으로 제작해보기로 하였는데요.
import numpy as np
import matplotlib.pyplot as plt
print("v=k[A]^m[B]^n 반응속도 계산프로그램")
print("---------------------------------------")
print("실험 I과 실험 II에서의 정보를 입력하세요")
print("(단, 실험 II에서의 농도가 더 높아야 함)")
print(" ")
print("실험 I에서")
M_ab1 = float(input("용액 A, B의 몰농도(M) : "))
L_a1 = float(input("용액 A의 양(L) : "))
L_b1 = float(input("용액 B의 양(L) : "))
W_1 = float(input("증류수 양(L) : "))
T_E1 = float(input("실험 I의 반응시간(s) : "))
print(" ")
print("실험 II에서")
M_ab2 = float(input("용액 A, B의 몰농도(M) : "))
L_a2 = float(input("용액 A의 양(L) : "))
L_b2 = float(input("용액 B의 양(L) : "))
W_2 = float(input("증류수 양(L) : "))
T_E2 = float(input("실험 II의 반응시간(s) : "))
M_N = np.log10(T_E2 / T_E1) / np.log10((M_ab1 / 2) / (M_ab2 / 2))
print(M_N)
M = int(round(M_N / 2, 1))
N = int(round(M_N / 2, 1))
print("반응차수 M = " + str(M) + ", N = " + str(N))
M = int(M)
N = int(N)
M_ab = float((M_ab1 + M_ab2) / 2)
M_n = M_ab * (L_a1 + L_b1) / (L_a1 + L_b1 + W_1)
V_ab = float(M_n / T_E1 / (M * N))
print("용액의 농도(M) = " + str(round(M_ab * (L_a1 + L_b1) / (L_a1 + L_b1 + W_1), 6)), )
print("반응속도(M/s) = " + str(round(V_ab, 6)), )
print("이 실험의 속도상수 k를 계산합니다")
k = float(V_ab / (np.power(M_ab1, M) * np.power(M_ab2, N)))
print("속도상수 k = " + str(round(k, 6)))
x = np.arange(0, 5, 0.1)
if M+N is 1:
y = x * k * 2 + T_E2
elif M+N is 2:
y = x * x * k * 2 + T_E2
elif M+N is 3:
y = x * x * x * k * 2 + T_E2
elif M+N is 4:
y = x * x * x * x * k * 2 + T_E2
else:
y = 0
plt.plot(x, y)
plt.show()
코드는 위와 같습니다. 언어는 python을 사용했고요. 그래프를 그려주는 matplotlib와 numpy 라이브러리를 사용했습니다. 제가 반응차수와 속도상수를 계산할 때 쓴 방법을 프로그래밍으로 옮긴 것인데요. 제가 계산할 때 실험 I-i와 I-ii를 비교해 위에서 속도상수 k=0.802, 반응차수는 m=n=1을 도출해냈었죠. 이를 프로그램을 실행시켜 입력하게 되면 아래와 같은 그래프가 출력됩니다.
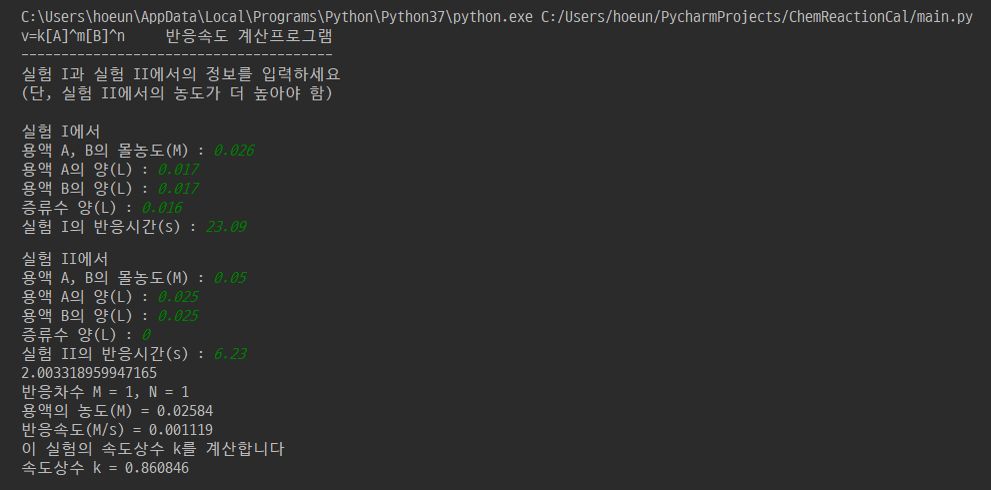

출력 결과는 위와 같습니다.
